17.3.2. Методологические основы исследования устойчивого динамического равновесия. «Золотое» правило накопления и дилемма государственной политики регулирования экономического роста
17.3.2. Методологические основы исследования устойчивого динамического равновесия. «Золотое» правило накопления и дилемма государственной политики регулирования экономического роста
Классическое направление исследует теорию устойчивой равновесной траектории. Основные постулаты данного направления:
каждый фактор производства обеспечивает соответствующую долю произведенного продукта, исследуется роль отдельных факторов роста с позиции количественного подхода (рост численности рабочих, основного капитала);
экономика обладает необходимыми предпосылками для автоматического восстановления в процессе свободной конкуренции, изучаются факторы производства с позиции качественного подхода (научные достижения, совершенствование образования, улучшения размещения организации производства).
Инструментом анализа является факторная функция:
y = W1L + W2K + W3n + a,
где y – темп прироста совокупного продукта;
W1, W2, W3 – доля L, K и природных ресурсов в совокупном продукте;
L, K, n – темп роста затрат труда, капитала, природных ресурсов;
a – темп роста научно-технического прогресса.
Цель анализа – выбор наиболее эффективной структуры и определение оптимального направления экономического роста.
Наиболее простой моделью экономического роста в классическом направлении является модель Солоу. Экономическими субъектами в модели являются домохозяйства и фирмы, постоянными параметрами будут рассмотрены: доля работающих в общей численности населения, темп роста населения, DN/N = n, доля амортизации – dK, удельный вес сбережений в национальном доходе Sy. Поскольку все факторы производства взаимозаменяемые, то капиталовооруженность меняется в различные временные лаги.
В условиях, когда технология производства неизменна, рассмотрим производственную функцию в расчете на душу населения у = f(кt), где кt = Кt / Nt – капиталовооруженность труда, Yt = Yt/Nt – производительность труда в период t.
Базовое уравнение накопления капитала в модели Солоу (рис. 17.12): kt = Sykt – (d + n)kt, где кt – изменение капиталовооруженности труда в момент t; Sy yt – доля сбережений на одного занятого в период t, n – прирост капитала, обусловленный приростом населения и занятых, d – доля обновляемого капитала на одного занятого.
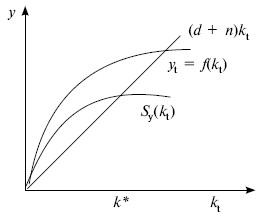
Рис. 17.12. Базовое уравнение накопления капитала в модели Солоу
В модели отражается концепция устойчивого стационарного состояния, когда при отсутствии технического прогресса и постоянной доли обновляемого капитала равновесие обеспечивает некоторый равновесный уровень капиталовооруженности (kt), при динамическом равновесии прирост капиталовооруженности должен быть равен нулю. Тогда Sy?(kt) = (d+n) kt.
Любое изменение удельного объема сбережений, связанное с приростом населения, должно соответствовать удельному приросту инвестиций St /Nt = ?It /Nt.
Данное условие соответствует динамическому равновесию при полной занятости.
Из модели Солоу можно выделить ряд положений, которые выступают либо условиями экономического роста, либо критериями оптимальности.
1. При устойчивом состоянии темп экономического роста определяется темпом роста трудовых ресурсов.
2. Технологические изменения в модели приводят к увеличению темпов экономического роста.
3. Уровень сбережений оказывает влияние на темпы роста в коротком периоде, в долгосрочном периоде, как правило, этого влияния может не быть.
4. Критерием оптимальности темпов экономического роста служит максимизация среднедушевого потребления («золотое» правило накопления). Экономический рост является эффективным, только если он приводит к максимальному из возможных уровней потребления. Однако, выбирая наибольшее потребление, необходимо найти варианты, которые не приводят к нарушению устойчивости стационарного состояния.
5. Для обеспечения оптимальных темпов экономического роста вся прибыль должна быть задействована в производстве.
Данный текст является ознакомительным фрагментом.