Эллипсы

Эллипс применяют в диаграммах, использующих логическое «И» (дерево текущей реальности, будущей реальности, перехода). Его задача – объединить несколько необходимых причин, которые в совокупности достаточны для возникновения некоторого результата (рис. 3.19). Если отсутствует любая из причин, объединенных эллипсом, то не будет иметь место и следствие этих причин, т. е. причинно-следственная связь нарушается. На практике разработчики пропускают сам эллипс, т. е. упускается существенное условие наступления некоторого события.

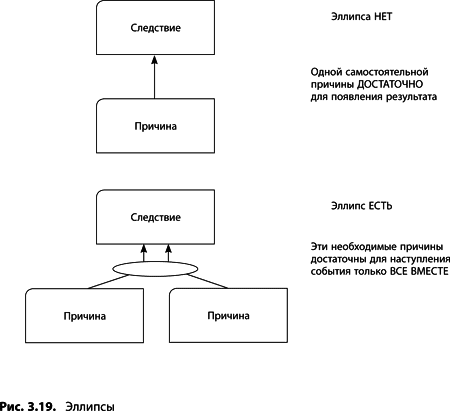
Вспомним недавний пример: «ЕСЛИ я выключаю свет, ТО в комнате темно». Вероятно, чтобы в комнате стало темно, недостаточно просто выключить свет (рис. 3.20). Можно добавить еще причину «ЕСЛИ в комнате нет окон», но и этого недостаточно, поэтому прибавляем «ЕСЛИ единственная в комнате дверь закрыта». Вот теперь это «строгое» построение.

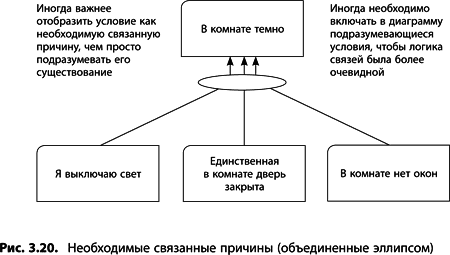
Помните, мир многогранен. У большинства явлений несколько причин, самостоятельных или взаимозависимых. Самостоятельной считается причина, которой самой по себе достаточно для наступления события. Если у одного явления имеется несколько самостоятельных причин, их обычно называют альтернативными (см. раздел «Альтернативная причина» в главе 2). Необходимая, но не достаточная причина может привести к появлению следствия только в совокупности с другими факторами, объединенными на рисунке эллипсом. Необходимо тщательно проверять существование связей и зависимостей между уже выстроенными утверждениями.

Примечание: нет необходимости включать в ДТР все до последней предпосылки или условия наступления события, иначе процесс построения сильно затянется и результат получится плохо читаемым. Всегда нужно ориентироваться на аудиторию, для которой вы создаете диаграмму. Если только для себя и в сфере, в которой вы хорошо ориентируетесь, можно многое помнить, не указывая на рисунке. Если же вам предстоит демонстрировать логическое дерево перед широкой аудиторией, подумайте, что именно вашим слушателям известно об изучаемом вопросе. Обычно представляемые публике диаграммы должны быть более подробными (меньше скрытых предположений; больше логических условий, объединенных эллипсом) – это поможет избежать недопонимания и путаницы.

Данный текст является ознакомительным фрагментом.