5.5. Параметрические методы ценообразования
5.5. Параметрические методы ценообразования
Параметрические методы ценообразования базируются на определении количественной зависимости между ценами и основными потребительскими свойствами товара, входящего в параметрический ряд. Параметрический ряд представляет собой группу товаров, которые однородны по функциональному назначению, конструкции, технологии изготовления, но имеют различия в потребительских характеристиках (например, для холодильников это мощность, размеры, объем морозильной камеры, энергоемкость и т. д.).
Эти методы используются при обосновании цен на новые изделия, а также для выявления соответствия уровня предполагаемой цены, рассчитанной на базе издержек производства, ценам, сложившимся на рынке.
Параметрические методы ценообразования включают метод сравнения удельных показателей, метод балльных параметрических оценок, метод корреляционно-регрессионного анализа, агрегатный метод.
Рассмотрим их содержание.
Метод сравнения удельных показателей используется для расчета цены на товары, потребительская ценность которых характеризуется одним главным потребительским параметром (мощность, производительность, вес, продолжительность службы и т. д.), а соотношение между товарами можно представить в виде формулы (5.33):
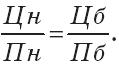
Тогда цена на новый товар рассчитывается (5.34):
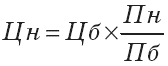
или (5.35):
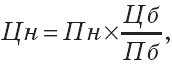
где Цн– цена нового товара, руб.;
Цб– цена базового товара, руб.;
Пб– значение основного параметра базового товара в принятых единицах измерения;
Пн– значение основного параметра нового товара в принятых единицах измерения;
Цб/Пб– удельная цена единицы основного параметра качества.
Этот метод является наиболее простым и применим к таким изделиям, где имеет значение какой-либо один, два параметра, а другие характеристики товара примерно одинаковы.
Пример 1. Определите цену на новую модель мини-трактора, если основными параметрами являются мощность двигателя и срок службы. Новая модель мощностью 100 л. с. имеет срок службы 10 лет. На рынке конкуренты предлагают аналогичный мини-трактор по цене 12 200 руб., мощность которого 80 л. с., срок службы 12 лет.
Решение
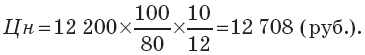
Метод балльных параметрических оценок. Товар i, который предприятие собирается реализовывать на рынке, оценивается по параметрам, имеющим значение для потребителей (материал, исполнение, фурнитура, мода и т. д.), и каждому параметру присваивается ранговый номер по значимости: 1, 2 и т. д.
Специалисты устанавливают для каждого изделия весовой индекс (%) в зависимости от значимости, причем общая сумма весовых индексов равна 100 %, и оценивают свое изделие и изделия конкурентов по 10-балльной системе. Умножив балл на весовой индекс и разделив на 100, получают оценку каждого параметра, сумма этих параметрических оценок дает общую параметрическую балльную оценку изделия Пi. Выбрав изделие какой-либо фирмы Э в качестве эталона (изделие, которое лучше всего реализуется на рынке, что свидетельствует о соответствии цены и качества) и приняв полученную им общую балльную оценку за 100 %, определяют оценочный процент Оi других изделий по формуле (5.36):
Оi = 100 : Пэ(взятого за 100 %) ? Пi.
Цену изделия i определяют по формуле (5.37):
Цi = Цэ x Оi : 100,
где Цэ – цена изделия, взятого за эталон, руб.
Метод корреляционно-регрессионного анализа. Суть этого метода состоит в определении зависимости изменения цены от изменения нескольких основных параметров качества в рамках параметрического ряда товара. При этом цену представляют в виде функции (5.38):
Ц = F (х 1 , х 2 … х),
где х1, х2… хn – выбранные основные параметры качества товара.
Для построения функции составляют параметрический ряд, т. е. накапливают исходную информацию о ценах и качественных характеристиках (параметрах) товаров. После статистической обработки исходных данных методом корреляционно-регрессионного анализа находят количественную зависимость между изменением цены и изменением параметров и строят регрессионное уравнение связи, которое может иметь различный вид:
линейное (5.39):
у = а 0 + ? аi xi;
степенное (5.40):
у = а0 +Пni xi;
параболическое (5.41):
у = а0 + ? аi xi + ? b i x2i,
где у – цена, руб.
Зная качественные характеристики товара и имея уравнение связи, определяют цену на него, подставляя в уравнение регрессии значение показателей.
Пример 2. Регрессионная зависимость между ценой и показателями качества шелковой ткани представлена в виде:
Ц = 266,5 + 0,48 х1 + 0,85 х2,
где х1– плотность 1 м2;
х2– доля натуральной нити,%.
Определите цену на новый вид шелковой ткани, плотность которой составляет 9 г на 1 м2, а доля натуральной нити – 80 %.
Решение
Ц = 266,5 + 0,48 ? 9 + 0,85 ? 80 = 338,82 (руб.).
Данный метод может успешно применяться в рыночной экономике, особенно для сложных изделий с большим параметрическим рядом, так как позволяет выявить зависимость цены от множества факторов, т. е. более обоснованно подходить к определению ее уровня.
Агрегатный метод заключается в суммировании цен отдельных конструктивных частей изделий, входящих в параметрический ряд, с добавлением стоимости новых деталей и нормативной прибыли.
Пример 3. Предприятие выпускает изделие стоимостью 285 руб., нормативная рентабельность продукции – 14 %. Изделие было модернизировано, затраты на модернизацию и добавление новой детали составили 36 руб. Определите цену нового изделия.
Решение
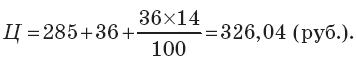
Параметрические методы целесообразно использовать на потребительском рынке, реализующем широко дифференцированные взаимозаменяемые товары.
Данный текст является ознакомительным фрагментом.