3. Веса агрегатных индексов цен и физического объема продукции

3. Веса агрегатных индексов цен и физического объема продукции

Агрегатная формула индекса товарооборота показывает, что его величина зависит от двух явлений, от двух переменных величин: физического объема товарооборота, т. е. количества проданных товаров, и цены за каждую единицу реализованных товаров. Чтобы выявить влияние каждой переменной в отдельности, следует влияние одной из них исключить, т. е. принять ее условно в качестве постоянной, неизменной величины на уровне отчетного или базисного периода. Вопрос о том, какой период принять в качестве постоянной величины, рассмотрим на примере индекса цен и индекса физического объема товарооборота.

Агрегатный индекс цен. Общее изменение цен можно определить, если считать постоянной величиной количество реализованных товаров за отчетный или базисный период. Если для получения индекса цен принимать в качестве весов данные о количестве реализованных товаров за отчетный период, можно получить следующую формулу агрегатного индекса цен:

где p₁ и р₀ – единицы реализованных товаров в отчетном и базисном периодах;

q₁ – количество реализованных товаров в отчетном периоде.

Если примем в качестве весов данные о количестве реализованных товаров в базисном периоде, то формула агрегатного индекса цен примет вид:

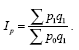
Полученные формулы агрегатных индексов цен с отчетными и базисными весами не идентичны.

Величина индекса зависит от индексируемых показателей, т. е от величин, изменения которых нам нужно определить, и от сомножителей, которые берутся в качестве весов, а в зависимости от данных, которые были взяты в качестве весов – это данные базисного или отчетного периодов, получают два разных индекса.

Первый индекс показывает изменение цен отчетного периода по сравнению с базисным по продукции, проданной в отчетном периоде, и фактическую экономию от снижения цен.

Другой индекс показывает, насколько поменялись цены в отчетном периоде по сопоставлении с базисными, но только по продукции, которая была реализована в базисном периоде, и экономию, которую можно было получить в результате снижения цен.

Абсолютная фактическая экономия от снижения цен в отчетном периоде определяется следующим образом:

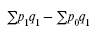
Абсолютная условная экономия в базисном периоде:

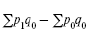
Для вычисления индекса цен необходимо сопоставить стоимость товаров, реализованных в отчетном периоде по ценам отчетного периода, со стоимостью этих же товаров, но по ценам базисного периода.

Агрегатный индекс цен представляет собой дробь, числитель и знаменатель которой состоят из двух сомножителей. Один из них является переменной индексируемой величиной (p₁ и p₀ ). а второй принимается условно в качестве постоянной величины – веса индекса (q₁ ).

Агрегатный индекс физического объема товарооборота

Индекс физического объема товарооборота представляет собой изменение физического объема в отчетном периоде по соотнесению с базисным. Чтобы агрегатный индекс показывал лишь изменение физического объема товарооборота, в качестве весов берутся неизменные цены базисного и отчетного периодов

Неизменные цены всегда только цены базисного периода. Применение в качестве весов неизменных цен дает возможность получить правильное представление о динамике физического объема товарооборота.

В индексе физического объема сомножитель индексируемого показателя берется на уровне базисного периода.

Формула агрегатного индекса физического объема продукции:

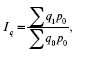
где ?q₁p₀ – стоимость продукции отчетного периода по ценам базисного;

?q₀p₀ – стоимость продукции базисного периода по ценам того же периода.

Абсолютное изменение физического объема вычисляется как разность между числителем и знаменателем индекса ?q₁p₀ – ?q₀p₀

Постоянные и переменные веса агрегатных индексов

Если индексы вычисляются за несколько периодов, то для всех них могут быть приняты одни и те же веса – индексы с постоянными весами, или же для каждого периода свои веса – индексы с переменными весами.

Теоретически возможны четыре типа индексов.

1. Общие базисные индексы цен с постоянными (базисными) весами:

2. Общие базисные индексы цен с переменными (отчетными) весами:

3. Общие цепные индексы цен с постоянными весами:

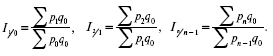
4. Общие цепные индексы цен с переменными весами:

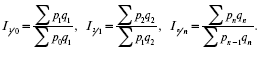
Эти индексы получены путем сопоставления цен каждого последующего периода с предыдущим, но взвешенных в каждом случае на количество товаров отчетного периода.

В этих индексах отражается как изменение цен за ряд последовательных периодов, так и изменение структуры реализованных товаров.

Для характеристики изменения цен по сравнению с начальным периодом без учета изменений в структуре произведенных товаров применяют общие базисные индексы с постоянными весами, в тех же целях, но с учетом изменения структуры – базисные индексы с переменными весами. Для определения изменения цен каждого периода по сравнению с предыдущим без учета изменений в структуре проданных товаров применяют цепные индексы с постоянными весами, с учетом изменений в структуре – цепные индексы с переменными весами.

Выбор периода взвешивания индексов зависит от того, какие индексы вычисляются: индексы количественных (объемных) или качественных показателей.

Данный текст является ознакомительным фрагментом.