8.2.2.3. Проблемы пакетных конкурентных торгов. Ограничения ставок
8.2.2.3. Проблемы пакетных конкурентных торгов. Ограничения ставок
Отличительной особенностью конкурентных торгов с пакетными заявками является их возможная сложность вычислений, поскольку даже в очень простой закупке количество комбинаций пакетов может быть очень высоким, как и количество поданных поставщиками ставок. Говоря точнее, в комбинаторных торгах количество предложений является экспонентной функцией количества закупаемых контрактов: если количество контрактов равно n, то общее количество ставок, которое может сделать один участник, равно 2n – 1. Поэтому, если в торгах участвуют N поставщиков, количество предложений, которое может получить закупщик, составит N(2n – 1). К примеру, если N = 3, а n = 4, то покупатель получит 15 ? 3 = 45 предложений. Если же количество контрактов повышается с n – 1 до n, количество возможных заявок повысится на N2n – 1, т. е. линейно для N, но экспоненциально (значительно быстрее) для n.
Таким образом, становится понятно, что управление комбинаторными торгами может быть очень затратным для закупщика из-за стоимости оценки (обработки) большого числа предложений и определения победителей. По этой причине проблема удобства вычислений может стать актуальной в случае принятия комбинаторных ставок.
Данные проблемы оправдывают введение потолка для общего количества ставок, которые может сделать участник. Ограничения количества предложений могут выражаться разными методами; несколько возможных мы рассмотрим ниже.
1. Если максимальное возможное количество предложений равно (2–1), то вне зависимости от самих ставок закупщик может ввести общий верхний лимит в n* < (2n – 1). Затем ограничение может установить, все ли ставки должны быть комбинаторными или нет.
2. Лимит на пакетные ставки. К примеру, если n = 5, участникам может быть разрешено подавать максимум одно предложение на каждый пакет с 5, 4, 3, 2 и 1 лотом.
3. Можно ввести структуру предложений, такую как так называемый «подсолнух». В этом случае участники имеют право подавать любое количество предложений при условии, что каждое из них содержит общий уникальный элемент (центр «подсолнуха», где пересекаются все предложения поставщика. – Примеч. научного редактора русского перевода). Применительно к аукциону автобусных маршрутов таким уникальным общим элементом для каждого поставщика становится наиболее важный для него маршрут, который он обязан включать во все подаваемые предложения.
Проблема «безбилетника»
В пакетных торгах поставщики, стремящиеся получить только отдельный контракт, могут «ездить бесплатно», т. е. могут намеренно подать высокую заявку, рассчитывая на агрессивное ответное поведение конкурентов. «Безбилетник» (free-rider) может, таким образом, победить в торгах, даже если более эффективно было бы распределить контракты по отдельности. Для иллюстрации этой проблемы рассмотрим следующий пример с тремя игроками и двумя лотами. (Как обычно, цифры соответствуют производственным издержкам участников.)
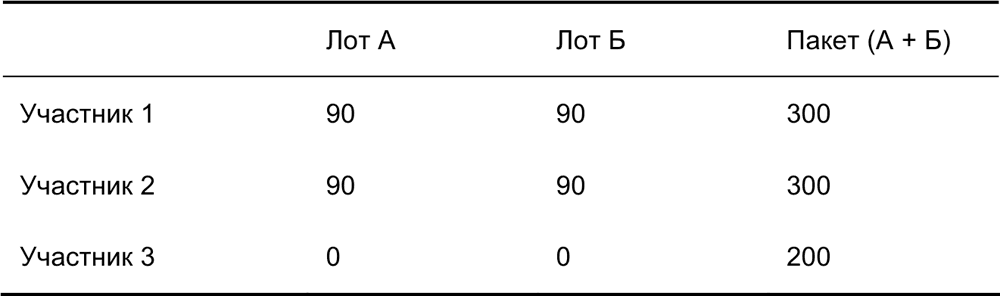
В этом примере закупщику удастся максимально сэкономить, присудив лот А первому поставщику за 90, а лот Б – второму тоже за 90 условных единиц.
Рассмотрим динамический обратный аукцион с пакетными ставками, обобщенный в SAA, и предположим, что в следующей таблице представлена ситуация на раунде t, где 0 соответствует отсутствию ставки.
Ставки в раунде t
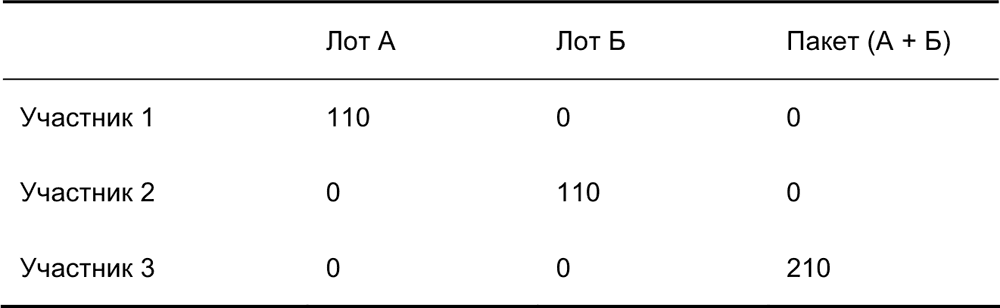
Учитывая текущие ставки, оба контракта будут отданы участнику 3. Тем не менее подобное распределение было бы неэффективным и экономически нецелесообразным для закупщика.
Участники 1 и 2 могли бы выиграть торги и опередить третьего игрока, снизив свои ставки, чтобы их сумма была меньше 200; однако каждый участник надеется, что ставку снизит конкурент. В результате, первый поставщик не захочет снижать свою ставку, если он ожидает от второго игрока понижения до 90. В общем, для получения одного из лотов каждый участник будет рассчитывать на агрессивное поведение другого для выведения третьего игрока из торгов. Но если ни один из них не снизит предложение, оба лота уйдут к участнику 3[219].
В случае актуальности проблемы «безбилетника» и высокой стоимости открытого аукциона закупщик должен провести SAA без пакетных заявок.
Данный текст является ознакомительным фрагментом.