2.5.5. Метод Монте-Карло

2.5.5. Метод Монте-Карло

Цель метода Монте-Карло (статистического анализа) состоит в определении степени воздействия случайных факторов на показатели эффективности проекта. Метод основан на сборе и обработке больших массивов данных как о проекте (компании), так и о внешней среде, с использованием статистических методов и моделей. На практике метод применяется редко.

Анализ производится следующим образом. Допустим, мы определили, какие именно данные следует признать неопределенными, а также установили диапазон значений, в пределах которого они могут изменяться случайным образом. Если речь идет, например, о двух параметрах, это означает, что определена область значений исходных данных, имеющая форму прямоугольника.

Для трех переменных эта область представляет собой параллелепипед, а для L-переменных – L-мерный параллелепипед. В любом случае совокупность исходных данных, от которых зависит судьба проекта, отображается точкой, лежащей внутри выделенной области. Таких точек великое множество, поэтому выполнить расчет проекта для каждой из них невозможно. Тем не менее необходимо определить, какое воздействие оказывает неопределенность исходных данных на поведение модели.

Предположим, в нашем распоряжении имеется способ выбирать точки в выделенной области данных случайным образом, аналогично рулетке в игорном заведении. Для каждой выбранной таким способом точки мы проведем расчет показателей эффективности и запишем их в таблицу. Проделав достаточно большое количество опытов, мы можем подвести некоторые итоги.

Для количественной оценки результатов используются два критерия: среднее значение и неопределенность.

Предположим, мы проделали N опытов и получили набор значений некоторого показателя fn (n = 1,…, N). Тогда среднее значение M определяется по формуле:

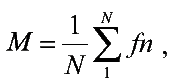
Неопределенность (или коэффициент вариации) рассчитывается следующим образом:

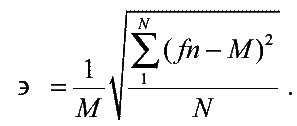
Величину М можно интерпретировать как ожидаемое значение случайной величины fn, а Э – как характеристику рассеяния значений fn. Чем меньше Э, тем ближе лежат значения fn друг к другу, тем точнее средняя величина М характеризует ожидаемое значение fn.

Неопределенность можно рассматривать так же, как оценку риска, связанного с тем, что значение fn отклонится от ожидаемой величины М.

Данный текст является ознакомительным фрагментом.