Расчет оптимального распределения

Расчет оптимального распределения

Прежде всего, давайте определимся с тем, что мы имеем в виду, когда говорим об оптимальном распределении. По сути, речь может идти об одном из трех видов распределения: будущем, гипотетическом или историческом. Вы можете определить оптимальный будущий состав портфеля не в большей мере, чем вырастить крылья и полететь, стать самым успешным игроком баскетбольной команды «Лейкерс» или завоевать титул «Мисс Америка». Любой, кто скажет вам, что он знает оптимальное будущее распределение, должен находиться в тюрьме или в сумасшедшем доме. (И если бы вы в действительности были способны на это, то эта книга не понадобилась бы. Вы бы знали будущую доходность по всем классам активов без всякого распределения активов. Вам потребовался бы только опытный водитель, чтобы возить вас в шикарном авто между вашими виллами в престижных курортных местечках.)

Гипотетическое оптимальное распределение относится к процессу постулирования набора доходностей, стандартных отклонений и корреляций для последующего расчета оптимального распределения при этих исходных данных.

Историческое оптимальное распределение, то есть то, что было оптимальным в прошлом, рассчитать можно. Это интересное упражнение, и мы скоро им займемся, но это очень плохой способ определения будущего распределения активов.

Мы уже намекнули на один из методов расчета исторического оптимального распределения. Вспомните «облака точек» для портфелей на рис. 4.9 и 4.10. Портфели с левого верхнего края облака лежат близко к границе эффективности и очень близки к оптимальным. Несложно создать электронные таблицы для исторических доходностей и поупражняться с вашими моделями распределения до тех пор, пока далее будет невозможно улучшать соотношение доходности и риска портфеля. По сути, большинство электронных таблиц содержит инструмент для оптимизации, позволяющий определить портфели, которые дадут вам максимальную (или даже минимальную) доходность при данном уровне стандартного отклонения или минимальное стандартное отклонение при данном уровне доходности. Это своего рода «оптимизатор бедняка». Однако эти методы довольно медленные и громоздкие, поэтому они не подходят человеку, серьезно изучающему теорию портфелей. Прежде всего они предполагают огромный объем работы, связанный с анализом «если» для выяснения того, что происходит при различных комбинациях доходности или стандартного отклонения актива. Изменить же корреляцию этого актива с другими активами почти невозможно.

Существует гораздо более быстрый и простой метод оптимизации портфелей – анализ среднего отклонения, разработанный несколько десятилетий назад Гарри Марковицем (впоследствии за эту работу он получил Нобелевскую премию). Пакет программ для использования этого метода называется оптимизатором среднего отклонения (MVO). MVO быстро рассчитает оптимальные составы портфелей по трем наборам данных.

1. Доходность каждого актива.

2. Стандартное отклонение каждого актива.

3. Корреляции всех активов.

До последнего времени MVO были дорогостоящими, но еще более дорогими были исходные данные. Из-за этого я потратил много усилий, описывая методы работы с электронными таблицами в предыдущем издании этой книги. К счастью, этого больше не требуется. MVO теперь можно получить по цене меньше $100, и получение данных также стало гораздо более простым делом. Информация о продуктах и продавцах приводится в Приложении А.

Одним из недостатков MVO является то, что он не учитывает восстановления баланса, поскольку это так называемый однопериодный метод, а восстановление баланса – многопериодное явление. Однако оптимальные портфели – одни и те же, независимо от того, проведено восстановление баланса или нет. Далее относительно легко произвести настройку с учетом восстановления баланса после расчета границы эффективности.

В качестве примера рассмотрим семь активов за период с 1970 по 1996 г., которые отражены на рис. 4.10, плюс долгосрочные облигации и казначейские векселя. Полные вводные данные для MVO для этого временного периода приведены в табл. 5.1.

Две первые колонки – это годовая доходность и стандартные отклонения. В соседних колонках приведены корреляции между годовой доходностью каждого актива за 27 годовых периодов.

Эти данные вводятся в оптимизатор, в нашем случае MVOPIus, производимый компанией Efficient Solutions. Как и во всех оптимизаторах Марковица, в этой программе используется метод критической линии для создания серии угловых портфелей, которые определяют построение границы эффективности для этого набора исходных данных. Рассмотрим результаты, представленные в табл. 5.2. На рис. 5.1 показаны реальные графические результаты работы MVOPIus.

Угловой портфель 1 – это портфель с минимальным отклонением; его риск минимален. Заметьте, что он состоит на 92,5 % из казначейских векселей и лишь на 7,5 % – из активов, которые мы обычно считаем довольно рискованными. Большинство портфелей в диапазоне риска, который большинство из нас сочло бы обоснованным, находится между угловыми портфелями 7 и 8. Портфели с 1-го по 6-й почти полностью состоят из краткосрочных обязательств, а выше портфеля 8 портфели становятся очень рискованными. Портфель 10 – портфель с максимальной доходностью.

Табл. 5.1. Исходные данные для оптимизатора, 1970–1996 гг.

^{Примечание: S&P-акции S&P 500; Мелк. – акции мелких компаний США (CRSP дециль 9-10); Европ. – акции европейских компаний (MSCI Europe); Аз. – Тих. – акции компаний Азиатско-Тихоокеанского региона (исключая Японию, MSCI Pacific ex-Japan); Япон. – акции японских компаний (MSCI Japan); Драг. – акции компаний, занимающихся добычей драгоценных металлов (объективная категория компании Morningstar); 20-лет. – 20-летние казначейские облигации США; 5-лет. – 5-летние казначейские билеты США; 30-дн. – 30-дневные казначейские векселя США.}

Табл. 5.2. Угловые портфели, 1970–1996 гг.

^{Примечание: S&P – акции S&P 500; Мелк. – акции мелких компаний США (CRSP дециль 9-10); Европ. – акции европейских компаний (MSCI Europe); Аз. – Тих. – акции компаний Азиатско-Тихоокеанского региона (исключая Японию, MSCI Pacific ex-Japan); Япон. – акции японских компаний (MSCI Japan); Драг. – акции компаний, занимающихся добычей драгоценных металлов (объективная категория компании Morningstar); 20-лет. – 20-летние казначейские облигации США; 5-лет. – 5-летние казначейские билеты США; 30-дн. – 30-дневные казначейские векселя США.}

Рис. 5.1. Выходные данные оптимизатора MVOPlus

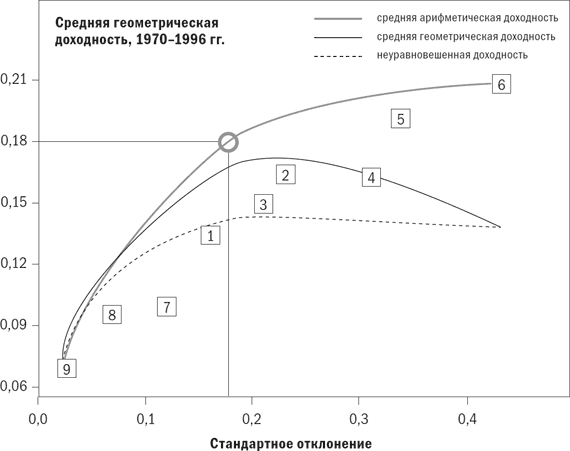
Математические подробности

MVOPlus обладает уникальной способностью определения портфеля с максимальной годовой доходностью (средней геометрической доходностью), в то время как все другие коммерческие оптимизаторы определяют актив с самой высокой средней арифметической доходностью в качестве последнего портфеля, который не является портфелем с максимальной средней геометрической доходностью. Это происходит потому, что разница между средней арифметической и средней геометрической доходностью равна примерно половине отклонения портфеля, или (SD)² / 2, и называется запаздыванием отклонения (variance drag). По мере движения вправо по графику соотношения доходности и риска запаздывание отклонения возрастает до точки, когда средняя геометрическая доходность начинает падать. Помните, что вы уменьшаете среднюю геометрическую доходность в годовом исчислении, а не среднюю арифметическую доходность.

Конечно, вы не ограничены угловыми портфелями. Если вы решите, что хотите оказаться на середине пути между портфелями 7 и 8, то просто усредняйте составы двух портфелей для каждого актива.

Взгляните на портфель 7. Он примерно на треть состоит из акций и на две трети из 5-летних казначейских билетов. Пока все вроде бы нормально. Но посмотрите на состав акций: почти исключительно акции мелких компаний США, японских компаний и компаний, занимающихся добычей драгоценных металлов. Это не тот портфель, которым хотел бы владеть любой разумный человек. Неслучайно в него вошли три актива, по которым получена самая высокая доходность за период с 1970 по 1996 г. Мы только что столкнулись с губительным недостатком оптимизации – излишним пристрастием к активам, имеющим в последнее время высокую доходность. По сути, после небольшой практики можно добиться от оптимизатора расчета почти любого желаемого портфеля. Измените данные о доходности по большинству активов на несколько процентов в любом направлении, и этот актив будет либо доминировать в портфеле, либо полностью исчезнет из него. Вы думаете, что можете спрогнозировать доходность по всем основным классам активов в своем портфеле? Если да, то вы и в самом деле очень талантливы. Следовательно, два фундаментальных закона оптимизаторов:

• оптимизатор явно предпочтет активы с высокой исторической или ожидаемой доходностью;

• если вы можете достаточно точно предсказать исходные данные оптимизатора для того, чтобы близко подойти к будущей границе эффективности, то оптимизатор вам не нужен.

Из приведенного примера должны быть видны риски необдуманного ввода в оптимизатор исторической доходности, стандартного отклонения и корреляций. Доходность актива склонна к тенденции иметь обратный смысл за длительные периоды времени: актив с выдающейся доходностью за последние 10 лет, скорее всего, будет иметь доходность ниже среднего в последующие 10 лет. Поэтому некоторые в шутку прозвали оптимизаторы максимизаторами ошибок.

Для лучшего понимания ошибок оптимизации посмотрим на то, что в действительности происходит при необдуманном вводе исторических данных в оптимизатор. Разделим период с 1970 по 1998 г. на несколько пятилеток и один четырехлетний период. Далее оптимизируем каждый пятилетний период и посмотрим, как оптимальное распределение активов, состоящих только из акций, будет вести себя в последующий пятилетний период по сравнению с «портфелем труса», состоящим из равных частей всех шести активов, представленных акциями (крупных компаний США, мелких компаний США, европейских компаний, компаний Азиатско-Тихоокеанского региона, японских компаний и компаний, занимающихся добычей драгоценных металлов).

Начнем с периода 1970–1974 гг. В этот период оптимальную доходность показывало следующее распределение: 99,8 % акций компаний, занимающихся добычей драгоценных металлов, и 0,2 % акций японских компаний; годовая доходность составляла 29,97 %. При переносе этого распределения на период с 1975 по 1979 г. получаем доходность в размере 14,71 % по сравнению с 25,38 % по «портфелю труса».

В 1975–1979 гг. оптимальным распределением было владение 100 % акций мелких компаний США; годовая доходность составляла 39,81 %. Это распределение, по сути, оказалось довольно эффективным при переносе на период с 1980 по 1984 г.: доходность составила 21,59 % по сравнению с доходностью «портфеля труса» в 14,75 %.

В 1980–1984 гг. оптимальным распределением было 73 % акций мелких компаний США и 27 % акций компаний, занимающихся добычей драгоценных металлов: доходность составляла 21,94 %. При переносе на период с 1985 по 1989 г. это распределение приносило доходность 11,83 % по сравнению с 24,14 % на «портфель труса».

В 1985–1989 гг. оптимальное распределение – 100 % акций японских компаний; оно приносило ошеломляющую годовую доходность в размере 40,24 %. Следующие пять лет? Минус 5,5 % по сравнению с +7,54 % по «портфелю труса».

Полезно вернуться на «машине времени» в конец 1980-х гг. Несколько квадратных миль недвижимости в Токио стоили больше, чем вся Калифорния, и скоро всем предстояло заговорить по-японски. «Доходность индекса Nikkei в сто раз больше? Просто люди с Запада не понимают, как оценивать акции на токийских рынках».

И, наконец, для периода с 1990 по 1994 г. лучшей стратегией распределения было владение 100 % акций компаний Азиатско-Тихоокеанского региона: годовая доходность составляла 15,27 %. В следующие четыре года (1995–1998) эта стратегия принесла убыток в 3,22 % против доходности «портфеля труса» в 6,61 %. И еще раз: в 1994 г. «все знали», что «азиатские тигры» достигнут американского уровня жизни за десять лет.

За весь период с 1975 по 1998 г. описанная выше пятилетняя стратегия оптимизации принесла бы годовую доходность в размере 8,40 %, что ниже доходности любого отдельно взятого актива, состоящего из акций, и намного ниже годовой доходности «портфеля труса» в 15,79 %.

Оптимизируя историческую доходность, вы на самом деле принимаете наиболее распространенную на современном этапе точку зрения. Это не совпадение. Рынки, прошедшие через период аномально высокой доходности, обычно претерпевали значительный рост цен, в разы больший роста дохода на акцию, и это почти всегда было следствием растущего оптимизма по отношению к данному активу.

Где мы находимся с нашим оптимизатором? В глубоком проигрыше. Мы не можем достаточно точно прогнозировать доходность, стандартное отклонение и корреляции, а если бы могли, то нам не был бы нужен оптимизатор. А оптимизация «сырых» исторических доходностей – билет в один конец в богадельню.

Итак, забудьте про получение ответа из магического черного ящика. Придется поискать последовательную стратегию распределения активов в другом месте.

Данный текст является ознакомительным фрагментом.