10.5.8. Дилемма олигополистов

10.5.8. Дилемма олигополистов

В анализе олигополистического ценообразования все чаще применяется теория игр. Рис. 10.15 помогает нам понять, почему сговор является трудным делом. Две фирмы являются единственными продавцами на рынке. Каждый может установить высокую ($5) или низкую ($3) цену.

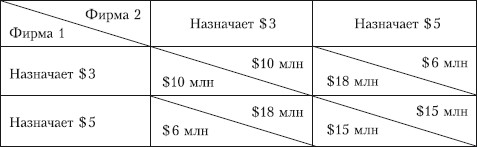
Рис. 10.15. Дилемма олигополистов

Если обе фирмы назначат одинаковые цены, то их прибыли также будут одинаковы (по $10 млн при цене $3 за штуку и по $15 млн при цене $5). Таким образом, в данной ситуации имеется побудительный мотив к сговору, но также и стремление к обману соперника. Если одна из фирм назначит низкую цену, а другая – высокую, то их прибыли будут сильно различаться: фирма, имеющая низкую цену получает $18 млн, а фирма, имеющая высокую цену, – $6 млн. долл.

Если фирмы могут действовать сообща, то ясно, что они обе назначат высокую цену. Если же каждая фирма действует независимо, стремясь максимизировать только свою собственную прибыль, то каждая установит цену более низкую, вне зависимости от того, что будет делать, по ее мнению, другая фирма. У каждой фирмы есть желание сбить цены своим конкурентам, зная, что конкуренты стремятся к тому же. Каково бы ни было желание сотрудничать, каждая фирма беспокоится (и не без основания), что если она будет конкурировать пассивно, ее соперник может конкурировать агрессивно, захватывая львиную долю на рынке.

В итоге молчаливый сговор недолговечен. Здесь изначально заложено недоверие друг к другу, и поэтому в любой момент может начаться олигополистическая война.

Анализируемая здесь базовая ситуация часто называется «дилеммой заключенных» и иллюстрируется проблемой, стоящей перед двумя содержащимися в отдельных камерах ворами, которые могут или сознаться, или не сознаться в краже, которую они совершили вместе. Когда каждый преследует исключительно собственные интересы, совместные действия заключенных приводят к наихудшему для обоих результату.

Преимущество теории игр перед другими моделями олигополии для практического использования заключается в том, что фирме не обязательно знать, какое решение примут ее конкуренты. Однако фирма должна уметь анализировать эффект каждого возможного решения. Очевидно, что эта задача практически невыполнима, когда на рынке действует много конкурирующих компаний. Следовательно, теория игр применима только в относительно простых случаях, но и при этом оценка прибыли, получаемой фирмой при каждом варианте, будет весьма приблизительна.

Примечания

Пусть отраслевой спрос представлен функцией Р = g – hQ; предложение продукции осуществляется двумя фирмами А и Б, при этом q_A + q_Б = Q. Затраты каждой фирмы составляют соответственно ТС_А = К_А + l_Аq_A и ТС_Б= К_Б + l_Бq_Б. Прибыль фирмы А определяется по формуле П_А = Рq_А – К_А – l_Аq_A = (g – hq_A – hq_Б) q_A – K_A – l_Аq_A. Она достигает максимума при g – 2hq_A – hq_Б = l_A. Отсюда следует, что фирма А максимизирует свою прибыль при объеме выпуска 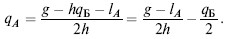. Это уравнение и есть уравнение реагирования фирмы А на объем выпуска ее конкурента. Аналогично 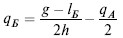уравнение реагирования фирмы Б на объем выпуска фирмы А.

Данный текст является ознакомительным фрагментом.