6 Некоторые дополнительные сложные случаи

6 Некоторые дополнительные сложные случаи

Когда экспансию начинают все банки одновременно

В свете того факта, что в данном контексте мы вынуждены предложить упрощенный взгляд на процесс кредитной экспансии, необходимо отметить несколько дополнительных моментов, а также сделать некоторые пояснения. Начнем с того, что описанные нами процессы экспансии целиком и полностью возникают исключительно в результате увеличения количества денег, внесенных на вклад в начальном банке (в нашем примере d представляет 1 000 000 д.е., депонированных в банке А). Однако и исторически, по мере развития банков, и в настоящее время все процессы кредитной экспансии характеризуются тем, что новые деньги вливаются в банковскую систему не через один-единственный банк, а через множество банков (а то и в той или иной степени через все банки системы). Как показывает Ричард Липси[282], кредитная экспансия, подобная описанной нами – происходящая ex nihilo и поддерживаемая созданием необходимых банковских депозитов, – будет повторяться всякий раз, когда в любом из банков будет делаться вклад в размере 1 000 000 д.е. Поэтому общий процесс экспансии на деле является более существенным по масштабам и качественно более сложным, так как он происходит одновременно во многих банках и от множества депозитов. В нашем единственном примере с коэффициентом резервирования 10 % в итоге были созданы кредиты на сумму 9 000 000 д.е., что в девять раз превышает начальный депозит, и в результате денежное предложение увеличивается в 10 раз. Главный вывод, который отсюда следует, состоит в том, что если все банки одновременно получат новые денежные депозиты, они смогут расширить кредит без уменьшения своих денежных резервов, потому что, предоставляя кредиты, ведущие к изъятию денег (как мы до сих пор предполагали в наших бухгалтерских записях), они одновременно получают депозит в виде части денег, предоставленных в виде кредитов другими банками. Следовательно, на деле вовсе не обязательно происходит значительное сокращение резервов каждого из банков, и каждый банк, поддерживая свои резервы практически в неприкосновенности, будет способен выдавать кредиты и соответственно создавать депозиты, без особого риска.

Этот теоретический аргумент побудил многих авторов, и в том числе Мюррея Ротбарда[283], при рассмотрении процесса кредитной экспансии в банковской системе исходить из того, что изолированный банк не теряет резервов при предоставлении все новых кредитов. Напротив, сохраняя резервы в неприкосновенности, изолированный банк изо всех сил пытается выдать новые кредиты на сумму, кратность которой по отношению к резервам обратно пропорциональна коэффициенту резервирования. Аргумент, объясняющий такой вид банковского мультипликатора, даже для случая изолированного банка, состоит в том, что банк будет пытаться избежать сокращения своих резервов в процессе предоставления кредитов (т. е. банкир не захочет оставить 100 000 д.е., а 900 000 д.е. ссудить). Напротив, для банка куда выгодней поддержание своего коэффициента резервирования путем предоставления кредитов на как можно более крупную сумму и сохранение начального резерва наличности в неприкосновенности (т. е. храня 1 000 000 д.е. наличными и создав из ничего новые кредиты на 9 000 000 д.е.). На практике уровень резервов наличности может быть обеспечен, если процесс кредитной экспансии протекает одновременно во всех банках. Это происходит оттого, что уменьшение наличности, которое банк испытывает после предоставления кредитов, компенсируется приемом новых депозитов, берущих начало из кредитов, взятых в других банках.

Процесс экспансии, представленный в таком виде, зачастую нелегко понять не только неспециалистам, но даже профессионалам банковского сектора, которые привыкли считать свой «бизнес» простым посредничеством между вкладчиками и заемщиками. Однако очевидно, что подход Ротбарда и других авторов совершенно корректен и заключается в том, что для наших целей не имеет значения, изучаем ли мы случай, рассмотренный выше (начальный вклад в размере 1 000 000 д.е. в банк А, расширившийся на всю банковскую систему), или банковскую систему из десяти банков, каждый из которых одновременно получает депозит в 100 000 д.е. (т. е. в общей сложности 1 000 000 д.е., поделенные на десять банков). В последнем случае каждый банк будет держать в неприкосновенности эти деньги, которые позволяют банкам расширять свои кредиты и создавать из ничего новые фидуциарные средства обращения на сумму 900 000 д.е. Каждый банк сможет поддерживать стабильные резервы наличности в размере 100 000 д.е., если возможное сокращение этих резервов в результате выдачи кредитов будет компенсироваться новыми депозитами, индуцированных кредитами, выданными другими банками. Поэтому если все банки одновременно принимают участие в экспансии, то каждый из них сможет держать свои резервы наличности в неприкосновенности, а с коэффициентом резервирования 0,1 они смогут произвести из ничего кредиты, обеспеченные фидуциарными средствами обращения, на сумму, в девять раз превышающую начальные депозиты. Рассмотрим этот процесс одновременной экспансии, отраженный в бухгалтерских записях.

Предположим, что каждый из десяти банков получил по 1 000 000 д.е. новых первичных денежных депозитов. Все десять банков одинакового размера, у каждого коэффициент резервирования c равен 10 %, и для простоты примем k равным нулю. Предположим также, что каждому банку принадлежит 10 % рынка. Иными словами, каждый банк получает 10 % общего числа клиентов рынка, на котором он действует. Более того, клиенты распределяются случайным образом. Если эти банки одновременно начинают расширять кредит по модели процесса, описанного в записи (42) и последующих, очевидно, что один из них – к примеру, банк А – в итоге получит депозиты, берущие начало от кредитов, выданных другими банками, как показано в табл. 4–2. Если все эти банки расширяют кредит одновременно, то записи в регистрах банка А будут следующими:

Уменьшение денежных средств нейтрализуется депозитом до востребования, сделанным конечным получателем средств из кредита, выданного, к примеру, банком В, что выражается в следующих записях:

Банк А в конечном итоге восстанавливает эти 810 000 д.е. в форме депозита, происходящего из кредитов, выданных, к примеру, банком С. Бухгалтерские проводки будут выглядеть так:

По мере продолжения этого процесса банк А получит депозиты от получателей кредитов, выданных банками D, E, F, G, H, I и J. В нашем объяснении мы крайне упростили этот процесс. В реальности банк получает в среднем 10 % от десяти кредитов в 900 000 д.е., выданных на первой стадии каждым банком системы. В этом случае банк А получит 10 % от десяти кредитов в 810 000 д.е., созданных каждым из банков на втором этапе, 10 % от десяти кредитов в 729 000 д.е., созданных каждым из банков на третьем этапе, и т. д.

Следовательно, если мы предположим, что каждый из десяти банков получает 1 000 000 д.е. в первичных вкладах и банки расширяют кредит одновременно, то баланс каждого из них – к примеру, банка А – будет выглядеть следующим образом:

Поэтому бухгалтерский баланс каждого банка совпадет с тем, что мы показали, предположив, что k = 1 (банк-монополист или банк, чьи клиенты – конечные получатели средств из выданных им кредитов). Так происходит вследствии того, что хотя в этом случае и нет монополии, но потеря денег, которую первоначально испытывает каждый из банков после расширения кредита, в конечном счете возмещается депозитами, берущими начало в кредитах, расширяемых другими банками.

Из баланса (53) можно сделать вывод, что для расширения кредитов каждому конкретному банкиру нет надобности уменьшать денежные резервы банка. Напротив, если остальные коллеги-банкиры будут расширять свой кредит в то же самое время, он сможет поддерживать уровень своих денежных резервов в неприкосновенности и непосредственно продолжать выдавать кредиты на сумму, в несколько раз превышающую его резервы. (В нашем случае каждый банкир держит 1 000 000 д.е. в денежных резервах и создает из ничего 9 000 000 д.е. в виде кредитов, обеспеченных вторичными депозитами на сумму 9 000 000 д.е.) Поэтому интерпретация Ротбардом данного процесса верна даже в случае изолированного банка, когда все остальные банки системы тоже получают первичные депозиты (т. е. пропорциональный объем новых денег, созданных системой) и все они расширяют кредит одновременно. Сумма денег, которой каждый банк теоретически должен лишиться при выдаче кредитов, компенсируется депозитами, получаемыми от получателей кредитов, выдаваемых коллегами банкира. Таким образом, каждый банк сможет самостоятельно расширить свой кредит на сумму 9 000 000 д.е. В свою очередь, общая экспансия системы составит 90 000 000 д.е., а общий объем депозитов, или предложения денег (денежной массы), достигнет 100 000 000 д.е.

К численным результатам, идентичным представленным в табл. 4–2, можно прийти, просто предположив, что в банк А сделан начальный депозит в размере 1 000 000 д.е. и разделен поровну между десятью банками системы, каждый из которых получает по 100 000 д.е. Эти 100 000 д.е. останутся неприкосновенными в хранилище каждого из банков. Каждый банк может расширять свой кредит до 900 000 д.е., и соответственно банковская система в целом может произвести 9 000 000 д.е. в виде новых кредитов, и в общей сложности 10 000 000 д.е. в первичных и производных депозитах.

Очевидно, этот последний пример, завершающий наш бухгалтерский анализ экспансии кредитов и депозитов изолированными банками и банковскими системами, более реалистичен. В нынешней кредитно-финансовой системе увеличение денежной массы пропитывает во всю банковскую систему и достигает практически всех банков, позволяя им расширять кредит одновременно, в соответствии с изученными нами процессами. Кроме того, существуют ясные исторические указания на то, что банки никогда не действовали в одиночку, но исключительно группами. Даже Саравиа-де-ла-Каллье упоминает, что банкиры основывали группы, предлагая «гарантов и действуя как гаранты друг для друга»[284]. Это означает, что во времена кастильских рынков XVI столетия банкиры уже были осведомлены об отношениях взаимозависимости и тесной общности интересов, объединяющих их в удачах и в неудачах их предприятий, понимая, что они нуждаются во взаимной поддержке друг друга.

Если говорить о золотом стандарте и увеличении денежного предложения в результате открытия новых золотых рудников и развития технологий добычи, то можно предположить, что новые деньги, возникающие в результате новых крупных открытий, первоначально достигают лишь некоторых банкиров и банков, откуда и распространяются по остальной банковской системе. Поэтому такие деньги инициируют процесс не одновременной экспансии, а постепенный процесс, посредством которого деньги просачиваются в систему в целом.

Таким образом, можно сделать вывод о том, что если имеется много банков и много новых депозитов и если банки расширяют свой кредит одновременно, то даже изолированный банк сможет поддерживать устойчивый уровень резервов и сам по себе расширять выдачу кредитов и создание депозитов кратно уровню резервов. При k = 0 объем этих кредитов и депозитов определяется как число, обратное коэффициенту резервирования[285]. Однако лишь по бухгалтерским записям становится очевидным, что депозиты обеспечивают богатство, присвоенное банкирами в ходе расширения своего кредита. С бухгалтерской (но не с юридической) точки зрения формальная собственность на эти кредиты принадлежит держателям депозитов, так как в обычных обстоятельствах они считают, что могут использовать деньги на своих депозитах (совершенный заместитель денег) в своих сделках без необходимости изымать физические денежные единицы. Тем не менее ясно, что активы, порожденные банковской системой, на деле не принадлежат никому. Однако их можно в большой степени считать собственностью акционеров, управляющих и директоров банков, т. е. тех, кто фактически извлекает пользу из этого богатства с тем дополнительным преимуществом, что они не являются его собственниками, так как согласно бухгалтерским книгам это богатство находится во владении вкладчиков.

Иными словами, в нормальных условиях депозиты, возникающие в связи с выдачей кредитов, – это просто вторичный результат того богатства, которое банки непрерывно накапливают и присваивают, результат, отраженный в бухгалтерских записях. К этой теме мы вернемся ниже при обсуждении проблемы банкнот, а также в последней главе этой книги, где будут представлены наши предложения по банковской реформе.

Вымывание денежного предложения из банковской системы

Другая сложность связана с тем, что всякий раз, когда выдается кредит и создается (и затем снимается со счета) депозит, определенная доля денежного предложения вымывается из системы и оседает у людей, которые не желают класть их на банковский депозит. Чем больше процент, который физически вымывается в карманы людей на каждой стадии и остается вне банковской системы, тем меньше способность банка генерировать новые кредиты.

Рассмотрим систему мелких банков (у которых k = 0) с коэффициентом резервирования 10 % (c = 0,1), обозначив через f долю денежного предложения, которая вымывается из банковской системы. Пусть f = 0,15. Когда банк А предоставляет кредит в размере 900 000 д.е., денежное предложение, которое должно вернуться в банковскую систему, будет равно:

(1 – f) 900 000 = (1–0,15) 900 000 = 765 000 д.е.

Поэтому, рассматривая систему мелких банков и приняв, что k = 0, c = 0,1, а f = 0,15, можно использовать следующие формулы:

если D_N – общая сумма чистых депозитов, которая состоит из брутто-депозитов D_G минус общая сумма денег, вымытых из системы, F, тогда:

[29] D_N= D_G– F.

Общая сумма денег, вымытых из системы, будет равна общей сумме брутто-депозитов D_G, умноженной на f, где f – процент денег, вымывающихся из системы. Таким образом,

[30] F= f·D_G.

В свою очередь, объем первоначально депонированных денег равен сумме чистых депозитов, умноженной на соответствующий коэффициент резервирования плюс общая сумма денег, вымытых из системы:

[31] d = D_N · c + F.

Подставив в это уравнение значение D_N из формулы [29] и значение F из формулы [30], получим:

[32] d= (D_G– F) · c+ f· D_G.

Заменив в уравнении F на f · D_G, получим:

[33] d= (D_G– f· D_G) c+ f· D_G.

Теперь вынесем за скобки D_G:

[34] d= D_G(c– cf+ f),

следовательно,

[35]

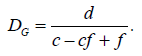
Так как D_N = D_G (1 – f), то

[36]

Это и есть формула чистых депозитов, созданных банковской системой. Кредитная экспансия, вызванная банковской системой, из которой вымываются деньги, будет равна:

[37]

Приравняв в предыдущих формулах f к нулю, получим те же уравнения, что использовались до сих пор для определения общего объема депозитов и общего объема кредитной экспансии:

[38]

и

[39]

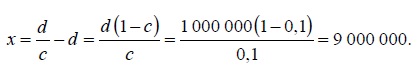
Теперь посмотрим, насколько уменьшится кредитная экспансия, если, как и ранее, d = 1 000 000 д.е., а c = 0,1, притом что 15 % денежной массы вымывается из банковской системы, т. е. (f = 0,15).

[40]

Следовательно, в банковской системе, где 15 % денежной массы вымывается за ее пределы, общая сумма депозитов составит 3 617 021 д.е., а не 10 000 000 д.е., как получается при f = 0.

Чистая кредитная экспансия будет равна

x = 3 617 021 – 1 000 000 = 2 617 021,

а не 9 000 000 д.е., создаваемых при условии, что деньги не вымываются из системы. Поэтому, когда доля утечки денег больше нуля, способность банковской системы производить кредиты и создавать депозиты из ничего существенно снижается[286].

Поддержание резервов, превышающих минимальные требования

Другое осложнение, вызывающее последствия, аналогичные рассмотренным в предыдущем разделе, возникает, когда банки поддерживают денежные запасы, превышающие минимальные требования. Эта тенденция проявляется на определенных стадиях экономического цикла, когда банки начинают вести себя осмотрительнее, или вынуждены увеличивать резервы ввиду нехватки достаточно кредитоспособных заемщиков, желающих получить кредит, или по обеим причинам. Так происходит, например, в фазах экономического спада, которые следуют за кредитной экспансией. Как бы то ни было, поддержание резервов наличности, превышающих необходимый уровень, снижает способность системы к кредитной экспансии точно так же как f, т. е. процент денег, вымывающихся из банковской системы[287].

Разные резервные требования для разных видов депозитов

И, наконец, можно рассмотреть еще одну проблему, которая связана с тем, что во многих странах резервные требования по депозитам до востребования отличаются от резервных требований по срочным депозитам, несмотря на то что, как нам известно, последние на практике часто являются истинными депозитами до востребования. Для депозитов обоих видов можно вывести рассмотренные нами выше формулы, однако их сложность перевешивает ту дополнительную пользу, которую они могли бы принести нашему анализу, поэтому мы решили обойтись без них[288].