31. Механическая и типическая выборки

31. Механическая и типическая выборки

При чисто механической выборке вся ге–неральная совокупность единиц должна быть прежде всего представлена в виде списка единиц отбора, со–ставленного в каком-то нейтральном по отношению к изучаемому признаку порядке. Затем список единиц отбора разбивается на столько равных частей, сколь–ко необходимо отобрать единиц. Далее по заранее установленному правилу, не связанному с вариацией исследуемого признака, из каждой части списка отби–рается одна единица. Этот вид выборки не всегда мо–жет обеспечить случайный характер отбора, и получен–ная выборка может оказаться смещенной. Объясняется это тем, что, во-первых, упорядочение единиц генеральной совокупности может иметь эл–емент неслучайного характера. Во-вторых, отбор из каждой части генеральной совокупности при непра–вильном установлении начала отсчета может также привести к ошибке смещения. Типическая (райониро–ванная, стратифицированная) выборка преследует две цели:

1) обеспечить представительство в выборке соответ–ствующих типических групп генеральной совокуп–ности по интересующим исследователя признакам;

2) увеличить точность результатов выборочного об–следования.

При типической выборке до начала ее формиро–вания генеральная совокупность единиц разбивается на типические группы. При этом очень важным момен–том является правильный выбор группировочного признака. Выделенные типические группы могут со–держать одинаковое или различное число единиц от–бора. В первом случае выборочная совокупность фор–мируется с одинаковой долей отбора из каждой группы, во втором – с долей, пропорциональной ее доле в генеральной совокупности. Если вы–борка формируется с равной долей отбора, по суще–ству она равносильна ряду собственно случайных вы–борок из меньших генеральных совокупностей, каждая из которых и есть типическая группа. Отбор из каждой группы осуществляется в случайном (повторном или бесповторном) либо механическом порядке. При ти–пической выборке удается устранить влияние меж–групповой вариации изучаемого признака на точность ее результатов, так как обеспечивается обязательное представительство в выборочной совокупности каж–дой из типических групп. Стандартная ошибка выбор–ки будет зависеть от величины средней из групповых дисперсий.

Поскольку средняя из групповых дисперсий всег–да меньше общей дисперсии, постольку при прочих равных условиях стандартная ошибка типической вы–борки будет меньше стандартной ошибки собственно случайной выборки.

При определении стандартных ошибок типиче–ской выборки применяются следующие формулы:

1) при повторном способе отбора:

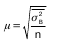
2) при бесповторном способе отбора:

 – средняя из групповых дисперсий в выбороч–ной совокупности

Данный текст является ознакомительным фрагментом.