3. Ошибки выборки

3. Ошибки выборки

Каждая единица при выборочном наблюдении должна иметь равную с другими возможность быть отобранной – это является основой собственнослучайной выборки.

Собственнослучайная выборка – это отбор единиц из всей генеральной совокупности посредством жеребьевки или другим подобным способом.

Принципом случайности является то, что на включение или исключение объекта из выборки не может повлиять любой фактор, кроме случая.

Доля выборки – это отношение числа единиц выборочной совокупности к числу единиц генеральной совокупности:

Собственнослучайный отбор в чистом виде является исходным среди всех других видов отбора, в нем заключаются и реализуются основные принципы выборочного статистического наблюдения.

Два основных вида обобщающих показателей, которые используют в выборочном методе – это средняя величина количественного признака и относительная величина альтернативного признака.

Выборочная доля (w), или частность, определяется отношением числа единиц, обладающих изучаемым признаком m, к общему числу единиц выборочной совокупности (n):

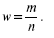
Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки.

Ошибка выборки, ее еще называют ошибкой репрезентативности, представляет собой разность соответствующих выборочных и генеральных характеристик:

1) для средней количественного признака:

?х =|х – х|;

2) для доли (альтернативного признака):

?w =|х – p|.

Только выборочным наблюдениям присуща ошибка выборки

Выборочная средняя и выборочная доля – это случайные величины, принимающие различные значения в зависимости от единиц изучаемой статистической совокупности, которые попали в выборку. Соответственно ошибки выборки – тоже случайные величины и также могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок – среднюю ошибку выборки.

Средняя ошибка выборки определяется объемом выборки: чем больше численность при прочих равных условиях, тем меньше величина средней ошибки выборки. Охватывая выборочным обследованием все большее количество единиц генеральной совокупности, все более точно характеризуем всю генеральную совокупность.

Средняя ошибка выборки зависит от степени варьирования изучаемого признака, в свою очередь степень варьирования характеризуется дисперсией ?² или w(l – w) – для альтернативного признака. Чем меньше вариация признака и дисперсия, тем меньше средняя ошибка выборки, и наоборот.

При случайном повторном отборе средние ошибки теоретически рассчитывают по следующим формулам:

1) для средней количественного признака:

где ?² – средняя величина дисперсии количественного признака.

2) для доли (альтернативного признака):

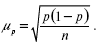
Так как дисперсия признака в генеральной совокупности ?² точно неизвестна, на практике пользуются значением дисперсии S² , рассчитанным для выборочной совокупности на основании закона больших чисел, согласно которому выборочная совокупность при достаточно большом объеме выборки достаточно точно воспроизводит характеристики генеральной совокупности.

Формулы средней ошибки выборки при случайном повторном отборе следующие. Для средней величины количественного признака: генеральная дисперсия выражается через выборную следующим соотношением:

где S² – значение дисперсии.

Механическая выборка – это отбор единиц в выборочную совокупность из генеральной, которая разбита по нейтральному признаку на равные группы; производится так, что из каждой такой группы в выборку отбирается лишь одна единица.

При механическом отборе единицы изучаемой статистической совокупности предварительно располагают в определенном порядке, после чего отбирают заданное число единиц механически через определенный интервал. При этом размер интервала в генеральной совокупности равен обратному значению доли выборки.

При достаточно большой совокупности механический отбор по точности результатов близок к собственнослучайному Поэтому для определения средней ошибки механической выборки используют формулы собственнослучайной бесповторной выборки.

Для отбора единиц из неоднородной совокупности применяется так называемая типическая выборка, используется, когда все единицы генеральной совокупности можно разбить на несколько качественно однородных, однотипных групп по признакам, от которых зависят изучаемые показатели.

Затем из каждой типической группы собственнослучайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность.

Типическая выборка обычно применяется при изучении сложных статистических совокупностей.

Типическая выборка дает более точные результаты. Типизация генеральной совокупности обеспечивает репрезентативность такой выборки, представительство в ней каждой типологической группы, что позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки. Поэтому при определении средней ошибки типической выборки в качестве показателя вариации выступает средняя из внутригрупповых дисперсий.

Серийная выборка предполагает случайный отбор из генеральной совокупности равновеликих групп для того, чтобы в таких группах подвергать наблюдению все без исключения единицы.

Поскольку внутри групп (серий) обследуются все без исключения единицы, средняя ошибка выборки (при отборе равновеликих серий) зависит только от межгрупповой (межсерийной) дисперсии.