8.4.2. Оптимальный путь роста

8.4.2. Оптимальный путь роста

Предположим, что цены ресурсов остаются неизменными, тогда как бюджет предприятия постоянно растет. Соединив точки касания изоквант с изокостами, мы получим линию 0G – «путь развития» (путь роста). Эта линия показывает темпы роста соотношения между факторами в процессе расширения производства (рис. 8.8).

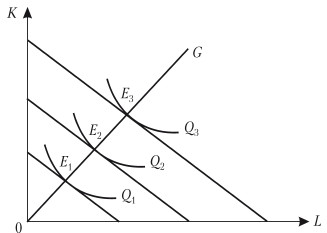
Рис. 8.8. Путь роста при постоянных ценах ресурсов и росте бюджета предприятия

В длительном периоде все производственные ресурсы переменны, и поэтому здесь в принципе не существует предела расширению производства.

Задача предприятия в этом случае сводится к задаче выбора оптимального пути роста. При данной производственной функции и данных ценах ресурсов, оптимальный путь роста определяется множеством точек касания соответствующих изоквант и изокост. Если производственная функция однородна, оптимальный путь роста определяется лучом, выходящим из начала координат, наклон которого определяет оптимальное соотношение К/L и зависит от соотношения цен ресурсов (рис. 8.9).

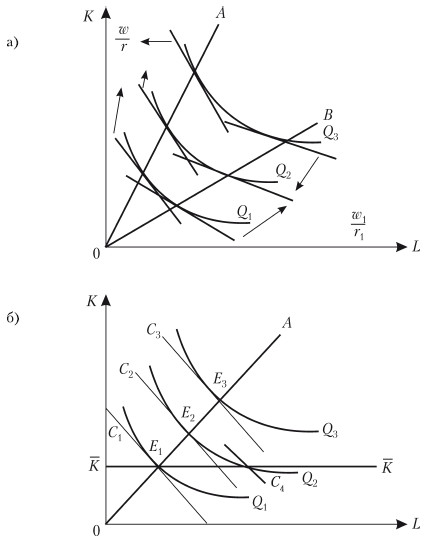
Рис. 8.9. Оптимальный путь роста

На рис. 8.9, а при соотношении цен w/r оптимальный путь роста определяется лучом ОА, а при соотношении цен w₁/r₁ – лучом ОВ. Понятно, что при изменении соотношения цен произойдет и изменение оптимального пути роста.

В коротком периоде (рис. 8.9, б) количество ресурса К фиксировано на уровне 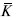и предприятие может расширять производство лишь за счет увеличения количества переменного ресурса, то есть вдоль линии 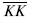, параллельной оси L. При данных ценах ресурсов их оптимальная комбинация недостижима. В самом деле оптимальным путем роста было бы движение вдоль луча ОА. Однако при фиксированном количестве постоянного фактора К точки Е₂ и Е₃ недостижимы, а рост производства возможен лишь вдоль линии 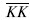. Очевидно, что при данных ценах увеличение выпуска в коротком периоде потребует более высоких затрат (изокоста С₄ расположена дальше от начала координат, чем изокоста С₂ при том же объеме выпуска Q₂).

Данный текст является ознакомительным фрагментом.