Методы приятия решений

We use cookies. Read the Privacy and Cookie Policy

Методы приятия решений

Почти все методы принятия решений в менеджменте с технической точки зрения можно считать разновидностями моделирования. Но традиционно термин модель обычно применяется только к общим методам, описанным выше, и к их многочисленным разновидностям. Кроме моделирования, существует еще ряд методов, помогающих менеджерам выбирать наиболее объективно обоснованные решения из нескольких альтернатив, в частности платежная матрица и дерево решений, описанные далее. Для повышения их эффективности и качества решений в целом менеджеры занимаются прогнозированием, о котором мы также поговорим далее. И опять наша цель – помочь вам постичь суть этих инструментов, а не научить применять их на практике.

Платежная матрица

Основная задача большинства управленческих решений заключается в выборе наилучшей из имеющихся альтернатив с учетом конкретных исходных критериев (см. главу 6). Платежная матрица – один из методов в статистической теории решений, помогающих руководителю выбрать альтернативу. Он особенно полезен при определении стратегии, наиболее подходящей для достижения конкретных целей.

По словам Н. П. Лумбы, «платеж представляет собой денежное вознаграждение или выгоду в результате использования конкретной стратегии в комбинации с конкретными состояниями природы. Представив платежи в форме таблицы (матрицы), мы получаем платежную матрицу». Пример такой матрицы вы видите на рис. 8.4. Слова «в комбинации с конкретными состояниями природы» очень важны для понимания того, когда используется платежная матрица и когда решение, принятое с ее помощью, будет действительно обоснованным. На базовом уровне это означает, что платеж обусловлен конкретными фактическими событиями. Если данное событие или состояние природы фактически не имеет места, платеж обязательно будет другим.

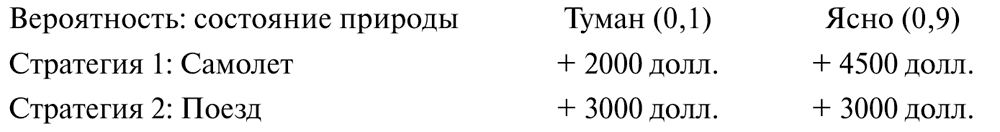
Представьте торгового агента, которому надо решить, лететь к потребителю самолетом или ехать поездом. Если погода позволяет, он может полететь и потратить на весь путь два часа; если придется ехать поездом, на дорогу уйдет семь часов, т. е. целый день работы, в течение которого он мог бы продать товаров на сумму 1500 долл. Предполагается, что иногородний потребитель, если его посетить лично, сделает заказ на 3000 долл. При этом, решив лететь к потребителю самолетом, агент рискует попасть в туман. Ему придется переждать в аэропорту, он так и не увидится с клиентом и будет вынужден общаться с ним по телефону. Это приведет к уменьшению заказа до пятисот долларов, но агент все же сможет генерировать продажи на сумму полторы тысячи долларов, вернувшись вовремя на рабочее место.

Представим ситуацию торгового агента, который решает, лететь ему самолетом или ехать к потребителю поездом. Если погода будет хорошей, он может лететь и потратить на всю дорогу 2 ч, а если придется ехать поездом – 7 ч. Если он поедет поездом, то потеряет день на месте его работы, который, по его оценке, мог бы увеличить сбыт на 1500 долл. По оценке иногородний потребитель должен сделать заказ на 3000 долл., если он лично посетит клиента. Если он запланирует лететь к клиенту, а потом самолет вынужден будет приземлиться из-за тумана, придется заменить личное посещение телефонным звонком. Это приведет к уменьшению заказа иногороднего клиента на 500 долл., но обеспечит заказы на 1500 долл. дома.

Данная платежная матрица отражает оценку последствий разных вариантов действий. Дополнительно представлены некоторые предположения относительно вероятности тумана (который скажется на самолете, но не на поезде) и ясной погоды. Мы видим, что вероятность ясной погоды в 10 раз выше, чем тумана. Далее, матрица показывает, что, действуя по первому варианту стратегии (самолет), если погода будет хорошей (9 шансов из 10), торговый агент по оценке продаст товаров на 4500 долл. (это и есть результат или последствия). Три других варианта последствий можно объяснить таким же образом.

Рис. 8.4. Платежная матрица.

Источник. Адаптировано по работе Martin К. Storr and Irving Stein, The Practice of Management Science (Englewood Cliffs, N.Y.: Prentice-Hall, 1976), p. 1. Воспроизводится с разрешения издателя.

Данные в приведенной выше платежной матрице отображают оценку последствий альтернативных действий. Кроме того, в нее включены предположения относительно вероятности тумана (из-за которого будет отменен полет, но который не скажется на путешествии поездом) и ясной погоды. Мы видим, что вероятность ясной погоды в десять раз выше, чем вероятность тумана. Далее, матрица отображает, что стратегия 1 (выбор самолета) при условии хорошей погоды (девять шансов из десяти) по предварительной оценке агента даст ему возможность достичь за исследуемый период объема сбыта в размере 4500 долл. (результат выбранного варианта). Точно так можно объяснить три остальных варианта.

В общем и целом, платежная матрица полезна в следующих случаях.

1. Количество альтернатив или стратегий, из которых делается выбор, разумно ограничено.

2. То, что может произойти, точно неизвестно.

3. Результаты решения зависят от того, какая выбрана альтернатива и какие события фактически имели место.

Кроме того, менеджеру надо уметь объективно оценивать вероятность релевантных событий и рассчитывать их ожидаемое значение. Менеджеры крайне редко имеют возможность наслаждаться полной определенностью, но редко оказываются и в условиях полной неопределенности. Почти всегда, принимая решения, они вынуждены оценивать вероятность события. Напомним, что степень вероятности варьируется от единицы, когда событие точно произойдет, до нуля, когда оно точно не произойдет. Вероятность можно оценить объективно, как, например, при игре в рулетку, но можно также базироваться на прошлых тенденциях или на субъективной оценке, основанной на опыте действий в похожих ситуациях.

Если не учесть вероятность, решение всегда будет «перекошено» в сторону наиболее оптимистического результата. Например, если исходить из того, что инвесторы в случае удачи фильма могут получить 500 % прибыли, а инвестиции в торговую сеть при самом лучшем раскладе принесут всего 20 %, то решение непременно будет принято в пользу фильма. Но если учесть, что вероятность безусловного успеха фильма довольно низка, а вероятность получения 20 % прибыли от инвестиций в торговлю очень высока, то второй вариант становится намного привлекательнее.

Вероятность играет важную роль и при определении ожидаемого значения – центральной концепции платежной матрицы. Ожидаемое значение альтернативы или стратегии – это сумма возможных значений, умноженная на соответствующие вероятности. Например, если вы считаете, что стратегия инвестирования в киоск со степенью вероятности 0,5 даст вам годовую прибыль 5 тыс. долл., с вероятностью 0,2 – 10 тыс. долл., и с вероятностью 0,3–3 тыс. долл., то ожидаемое значение составит

5000 (0,5) + 10 000 (0,2) + 3000 (0,3) = 5400 долл.

Определив ожидаемое значение каждой альтернативы и расположив полученные данные в виде матрицы, менеджер без труда оценит, какой вариант наиболее привлекателен при конкретных заданных критериях. Ясно, что это будет вариант с самым большим ожидаемым значением. Исследования показали, что, если вероятность определена точно, дерево решений и платежная матрица позволяют принимать более правильные решения, чем традиционные методы.

Дерево решений

Дерево решений – еще один популярный метод для выбора наилучшего альтернативного направления действий в менеджменте. «Дерево решений – схематичное представление проблемы принятия решений.» Подобно платежной матрице, этой метод позволяет менеджерам «оценить разные направления действий, объединить их с финансовыми результатами, изменить эти результаты с учетом вероятности и сравнить альтернативы». Концепция ожидаемого значения является неотъемлемым элементом и этого метода.

Дерево решений можно использоваться в ситуациях, подобных описанной при обсуждении платежной матрицы, т. е. если предполагается, что данные о результатах, степени вероятности и т. д. на последующие решения не повлияют. В этом случае менеджер принимает единичное решение. Но дерево решений позволяет проанализировать более сложную ситуацию, когда результаты одного решения влияют на последующие. Следовательно, это весьма полезный инструмент для принятия последовательных решений.

На рис. 8.5 показано, как используется дерево решений. Вице-президент фирмы, выпускающей электрические газонокосилки, считает, что рынок ручных приспособлений данного типа растет. Ему надо решить, следует ли начать выпуск ручных косилок, и если следует, то стоит ли продолжать выпускать электрические. Производство устройств обоих типов потребует расширения производственных мощностей. Руководитель собрал необходимую информацию об ожидаемых последствиях разных вариантов действий и о вероятности событий, которую представил в виде дерева решений.

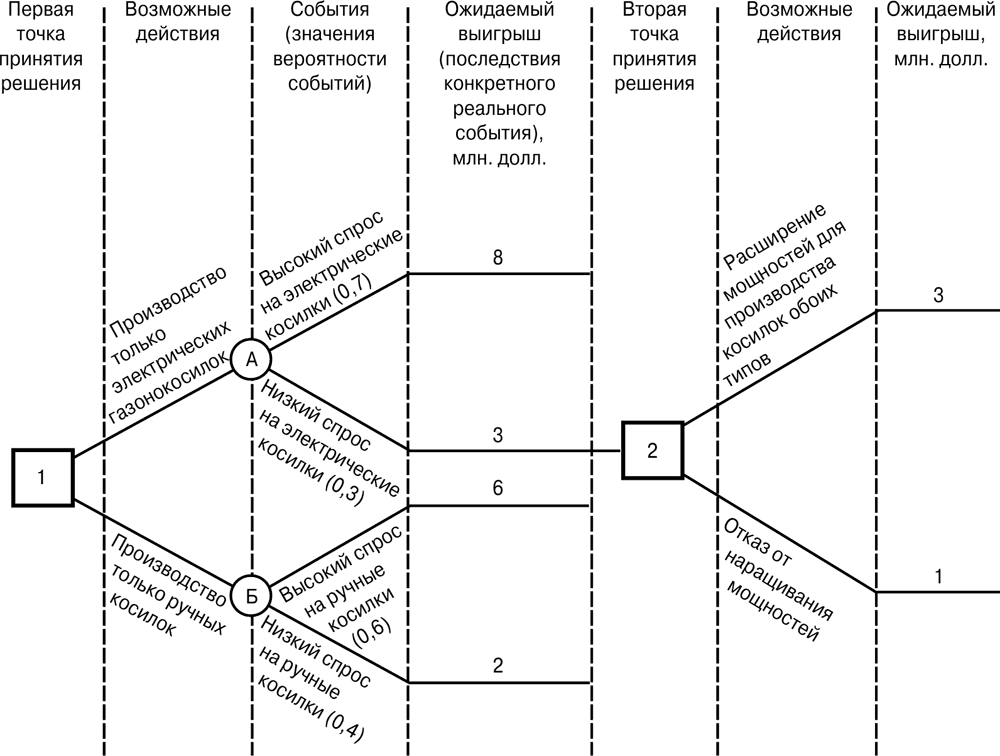
Рис. 8.5. Дерево решений.

Используя дерево решений, менеджер идет назад от второй точки принятия решения. Самое желательное решение в этой точке – расширить производственные мощности и начать выпускать газонокосилки обоих типов. Оно обусловлено тем, что в этом случае ожидаемая прибыль (3 млн. долл.) превышает прибыль (1 млн. долл.) в случае отказа от расширения производства при условии, что в точке А спрос на электрокосилки будет низким.

Менеджер продолжает идти назад к текущему моменту (к первой точке принятия решений) и рассчитывает ожидаемые значения при разных альтернативных действиях – если будет решено производить только электрические или только ручные устройства. Ожидаемое значение в первом случае составляет 6,5 млн. долл. (0,7 ? 8 млн. долл. + 0,3 ? 3 млн. долл.); при выборе второго варианта этот показатель будет всего 4,4 млн. долл. Следовательно, расширение производства с целью выпуска косилок обоих типов является самым желательным решением, так как ожидаемая прибыль, если все случится так, как ожидается, будет наивысшей.

Данный текст является ознакомительным фрагментом.