Время улыбаться и время печалиться
Время улыбаться и время печалиться
Нелинейность бывает двух видов: вогнутая (обращенная внутрь), как в примере с царем и камнем, и выпуклая (обращенная вовне). Встречаются, конечно, и смешанные, выпукло-вогнутые случаи.
На рисунках 10 и 11 показана упрощенная нелинейность: выпуклость и вогнутость похожи соответственно на улыбающееся и грустное лицо.
Рис. 10. Два типа нелинейности, выпуклая (слева) и вогнутая (справа). Выпуклая дуга выгибается по направлению вовне, вогнутая – внутрь.
Рис. 11. Улыбайтесь! Лучший способ понять выпуклость и вогнутость. То, что выгнуто вовне, выглядит как улыбка, а то, что выгнуто внутрь, кажется грустным лицом. Выпуклое (слева) антихрупко, вогнутое (справа) хрупко (страдает от эффекта негативной выпуклости).
Чтобы упростить рассуждения, я использую термин «эффект выпуклости» для обоих случаев: в одном случае это «эффект позитивной выпуклости», в другом – «эффект негативной выпуклости».
Почему асимметрия сводится к выпуклости и вогнутости? Это просто: если для данной вариации приобретения больше, чем потери, и вы нарисуете ее график, он будет выпуклым; обратный график будет вогнутым. На рис. 12 показана асимметрия, выраженная в терминах нелинейности. Там очевиден и волшебный эффект математики, позволяющий одним графиком охватить татарский бифштекс, предпринимательство и финансовый риск: выпуклый график превращается в вогнутый, когда перед формулой ставишь знак «минус». Например, от некоей сделки Жирный Тони и какой-нибудь банк или фонд получают обратные результаты: Тони зарабатывает доллар всякий раз, когда банк его теряет, и наоборот. По большому счету прибыль и убыток – зеркальные отражения друг друга, только где у одного плюс, там у другого минус.
Рисунок 12 также демонстрирует, почему выпуклое любит переменчивость. Если на переменах вы больше зарабатываете, чем теряете, вам будет хотеться перемен.
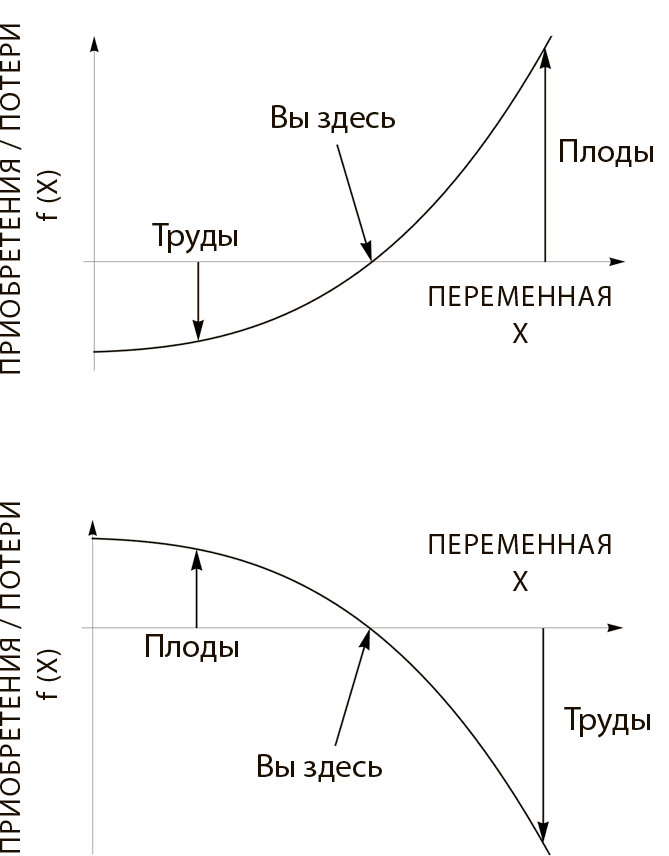
Рис. 12. Больше трудов, чем плодов, или больше плодов, чем трудов. Предположим, вы начинаете движение из точки «вы здесь». В первом случае при увеличении переменной «х», то есть при движении вправо по горизонтальной оси, приобретения (вертикальная ось) будут больше, чем потери при движении влево, иными словами, при эквивалентном уменьшении переменной «х». Рисунок демонстрирует, как позитивная асимметрия (график слева) преобразуется в выпуклую (выгнутую внутрь) кривую, а негативная асимметрия (график справа) – в вогнутую (выгнутую вовне) кривую. Повторим: при эквивалентных изменениях переменной в обоих направлениях выпуклость дает больше, чем отбирает, а вогнутость – наоборот.
Данный текст является ознакомительным фрагментом.