Более общая методология распознавания ошибки модели

We use cookies. Read the Privacy and Cookie Policy

Более общая методология распознавания ошибки модели

Эффекты второго порядка и хрупкость модели. Предположим, у нас имеется работающая модель (это великодушное предположение), но мы не уверены в том, что нам известны ее параметры. Как и в примере с дефицитом/занятостью в предыдущем разделе, мы используем f, простую функцию:

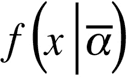
где ? – это средняя ожидаемая вводимая переменная. Пусть ? – это распределение ? в области ,

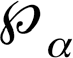Философский камень. Одно то, что параметр ? неопределен (поскольку у нас есть только его оценка), может исказить результат, если мы станем изменять этот параметр внутри интеграла, то есть стохастизируем параметр, который, по предположению, был фиксирован. Соответственно, мы можем легко измерить склонность к выпуклости как разницу между (а) значением функции f, интегрированной в области потенциальных значений ?, и (б) значением функции f для единственного значения ?, которое мы считаем его средним значением. Следовательно, склонность к выпуклости (философский камень) ?A – это[138]:

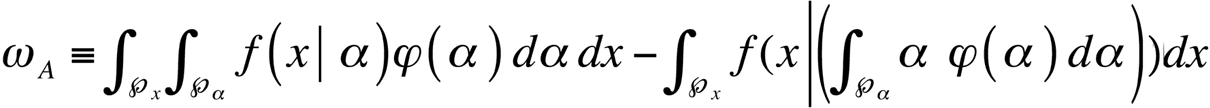
Основное уравнение. Хрупкость – это частичный философский камень в промежутке до K, отсюда неучтенная хрупкость ?B оценивается путем сравнения двух интегралов, взятых в промежутке до K, чтобы выявить эффект левого хвоста:

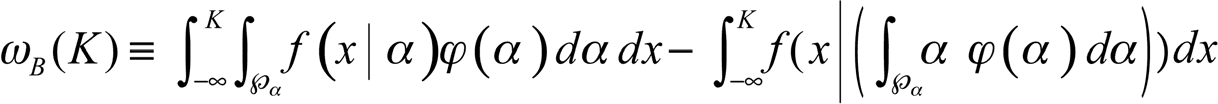
Эту формулу можно приблизительно оценить, используя интерполяцию, взятую между двумя значениями ?, которые отделены от среднего значения 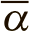средним отклонением ?, то есть ??. В результате получим оценку:

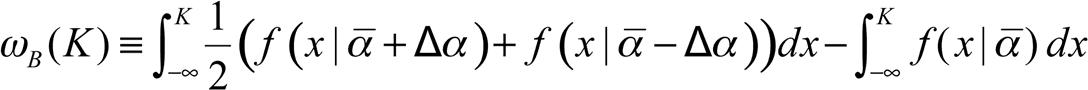
Антихрупкость ?C есть интеграл, посчитанный на промежутке K до бесконечности. Мы можем изучить ?B путем точечных оценок для X ? K.

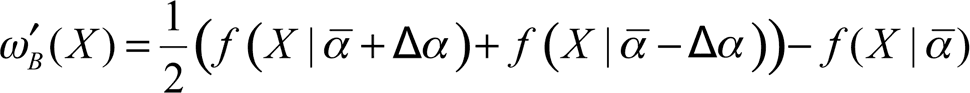
откуда:

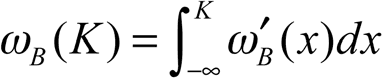
что приводит нас к эвристическому правилу распознания хрупкости (Taleb, Canetti, et al., 2012). В частности, если ??B (X) не меняет знак для X ? K, то ?B (K) будет иметь тот же знак. Распознать хрупкость можно по поведению в хвостах, для чего следует проверить функцию ??B (X) для любого X.

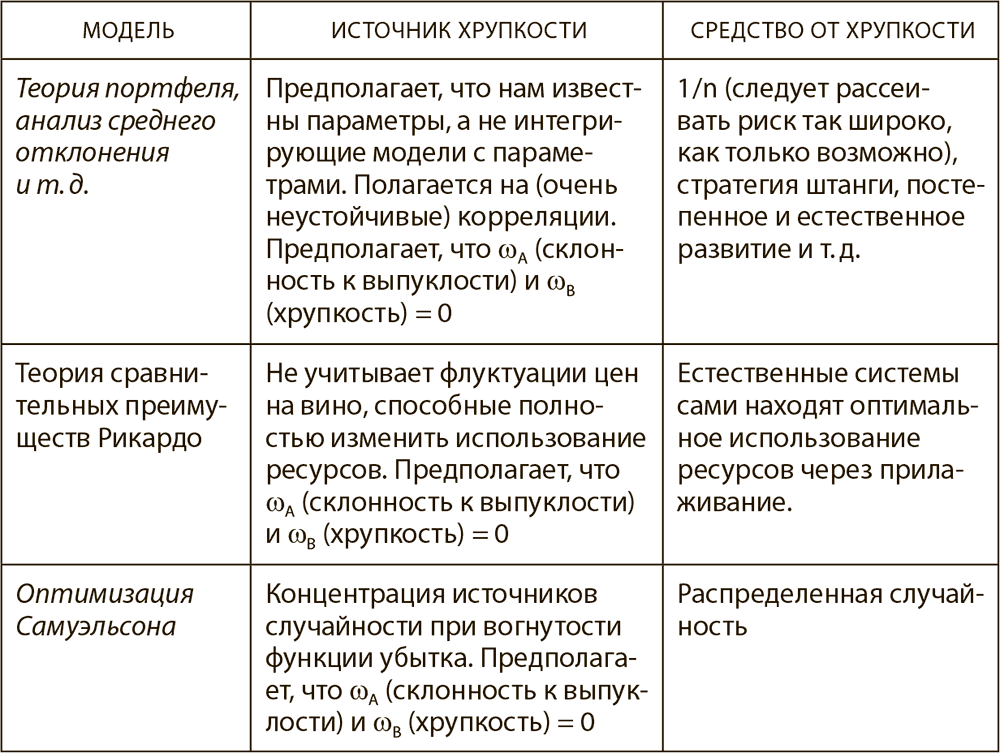
Таблица 12

Заблуждения, связанные с портфелем ценных бумаг. Среди тех, кто верит Марковицу, распространено одно заблуждение: теория портфеля побуждает диверсифицировать вложения, следовательно, она лучше, чем ничего. Неправда, придурки от финансов: она побуждает оптимизировать, то есть вкладывать в ценные бумаги больше денег, чем следует. Эта теория не побуждает рисковать меньше за счет диверсификации, она заставляет открывать больше позиций только потому, что у них есть компенсирующие статистические свойства, а значит, порождает риск ошибки модели – и очень большой риск недооценки хвостовых событий. Что понять, как это происходит, представьте себе двух инвесторов, выбирающих три объекта для размещения средств: наличные деньги, ценные бумаги А и ценные бумаги В. Инвестор, не знающий статистических свойств А и В и понимающий, что он их не знает, разместит часть средств, которую не хочет терять, в наличности, а остальное в А и В – в зависимости от эвристики, которую он привык применять. Инвестор, полагающий, что он знает статистические свойства А и В, то есть параметры ?A, ?B, ?A, B, вложит в ценные бумаги ?A и ?B так, чтобы суммарный риск был на желаемом уровне (ожидаемую отдачу мы в расчет не берем). Чем более занижена в его восприятии корреляция ?A, B, тем худшему риску ошибки модели он подвержен. Полагая, что корреляция ?A, B равна 0, инвестор вложит в ценные бумаги на треть больше средств, чем следует, если брать в расчет маловероятные события. Если же бедный инвестор питает иллюзию, что корреляция равна –1, он максимально инвестирует в A и B. И если он вдобавок использует леверидж, его ждет та же печальная судьба, что постигла фонд Long-Term Capital Management, одураченный как раз параметрами. (В реальности, в отличие от статей об экономике, ситуация обычно меняется; ради Баала, она меняется!) Мы можем повторить то же рассуждение для каждого параметра ? и посмотреть, как заниженная оценка этой ? ведет к избыточному размещению средств.

Работая трейдером, я заметил – и эта идея меня не отпускала, – что значения корреляций на разных временных промежутках никогда не совпадают. Нестабильные – это для них слишком мягкое слово: 0,8 в течение одного долгосрочного периода превращается в —0,2 в течение другого долгосрочного периода. Лохотрон чистой воды. Когда рынок напряжен, корреляции меняются еще быстрее – без какой-либо очевидной регулярности, несмотря на все попытки смоделировать «кризисные корреляции». Taleb (1997) изучает эффект стохастических корреляций: чувствовать себя в безопасности может лишь тот, кто играет на понижение при корреляции 1 и покупает при —1 – что вполне соответствует эвристическому правилу 1/n.

Критерий Келли против Марковица. Чтобы применить оптимизацию а-ля Марковиц во всей ее полноте, необходимо знать полное совместное распределение вероятностей всех активов до конца времен – плюс точную функцию полезности для благосостояния до конца времен. И без погрешностей! (Мы видели, что погрешность оценки взрывает систему.) Метод Келли, разработанный почти одновременно с теорией Марковица, не требует ни совместного распределения, ни функции полезности. На практике инвестору нужно знать соотношение ожидаемой прибыли к отдаче в худшем случае – динамически скорректированное, чтобы избежать катастрофы. В случае с трансформациями штанги худшая отдача гарантирована. И ошибка модели для критерия Келли куда меньше. См. Thorp (1971, 1998), Haigh (2000).

Замечательный Аарон Браун считает, что экономисты отвергли идеи Келли – невзирая на их практическую привлекательность, – из-за любви к общим теориям ценообразования.

Ограниченный метод проб и ошибок совместим с критерием Келли, когда инвестор имеет представление о потенциальной отдаче. Даже если нельзя сказать, какой будет отдача, в случае, если потери ограничены, результат будет неуязвим, так что этот метод должен превзойти теорию хрупкодела Марковица.

Корпоративные финансы. Если коротко, корпоративные финансы обычно прогнозируются точечно, а не дистрибутивно. Если мы введем, скажем, в модель оценки Гордона неустойчивый прогноз денежных потоков, заменив заданный – и известный – рост (и другие параметры) постоянно скачущими переменными (особенно при распределениях с жирными хвостами), предполагаемая стоимость компаний, которые считаются дорогими или растут быстро, но зарабатывают мало, может значительно повыситься. Рынок оценивает их именно так эвристически, без какой-либо явной причины.

Заключение и вывод. Истеблишмент экономической науки так и не понял, что если у нас имеется работающая модель (а это крайне великодушное предположение), но мы не уверены в ее параметрах, это неизбежно приведет к увеличению хрупкости в условиях выпуклости и нелинейности.

Данный текст является ознакомительным фрагментом.