УСКОРЕНИЕ РОСТА В ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ (УСТРАНЕНИЕ АСИММЕТРИЧНОГО ДЕЙСТВИЯ РЫЧАГА)

Это другая функция ускоренной ставки снижения. При правильном использовании эта стратегия может существенно увеличить прибыли. Чтобы проиллюстрировать отрицательный эффект асимметричного действия рычага (и, следовательно, наличие возможности для его устранения), мы вернемся к примеру с подбрасыванием монеты, описанному во второй главе.

Оптимальная фракция составляет реинвестируемые 25% прибыли при каждом подбрасывании монеты. В таком варианте полученное значение прироста равняется 36.100 долларам в сравнении с 4.700 долларами, получаемыми от 10 и 40%. Вспомните также, что эта функция характеризуется гауссовой кривой. Все точки слева и справа от оптимальной фракции не давали такой прибыли, которую генерировала оптимальная фракция. Гауссова кривая возникает в результате асимметричного воздействия рычага. Исключите из картинки асимметричное действие рычага, и у вас получится совсем иная ситуация.

Асимметричное действие рычага просто сокращает возможность компенсировать убытки. Если число торгуемых контрактов равно двум и после издержек уменьшается до одного, то возможность компенсировать убытки снижается на 50%. Если потери составляют 1.000 долларов на контракт, то общий убыток составит 2.000 долларов. Если следующая сделка приносит прибыль 1.000 долларов, но лишь для одного контракта, то для компенсации убытка по двум контрактам потребуется еще одна сделка с 1.000 долларов прибыли. Чтобы избежать этого, просто не сокращайте число контрактов.

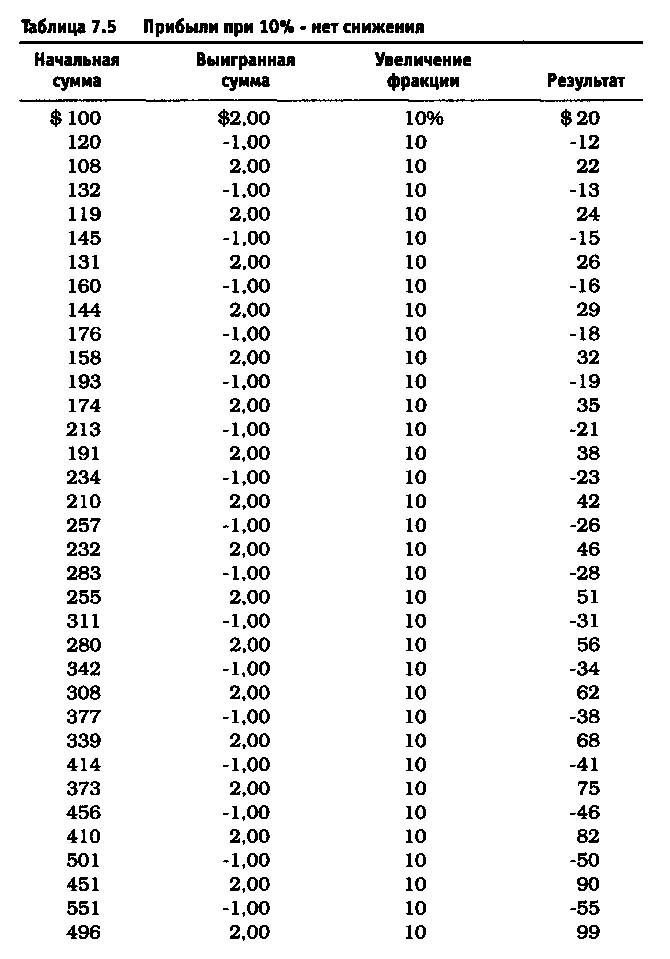
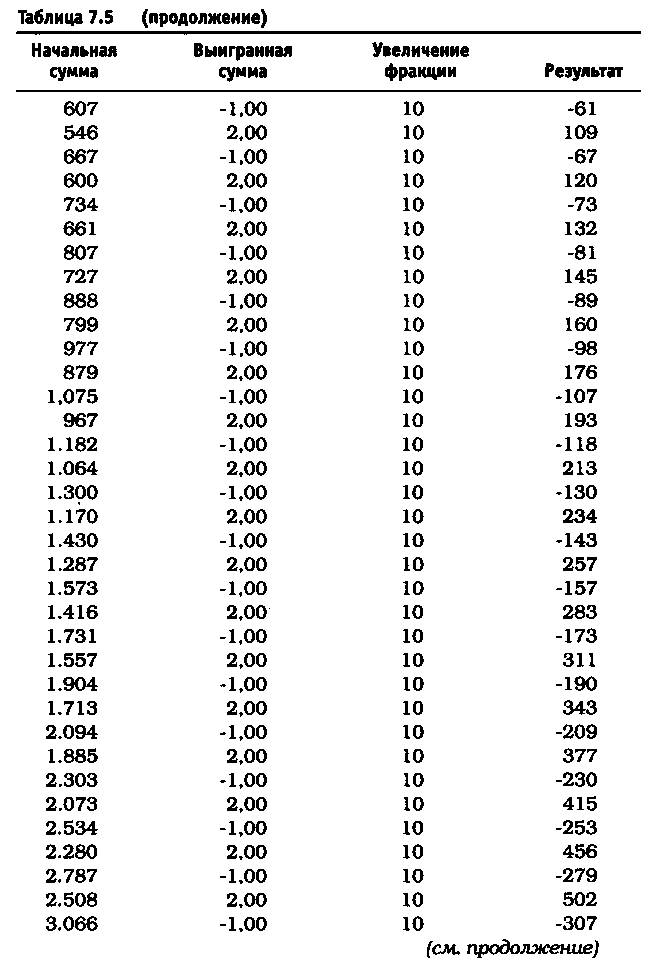
Вспомним пример с монетой: торговля 10% баланса счета означает, что величина следующей торговли — это произведение баланса и 0,10. Если начальный счет составляет 100 долларов, то величина риска в следующей сделке составит 10 долларов. Если торговая сделка оказывается удачной, то выигрыш принесет 2 доллара на каждый доллар суммы риска. Убыток от проигрышной сделки составит по 1 доллару на каждый доллар, подвергаемый риску. Счет либо увеличивается на сумму выигрыша, либо уменьшается на величину проигрыша, и после этого производится перерасчет для следующей сделки (или подбрасывания монеты). В случае выигрыша размер счета вырастает со 100 до 120 долларов. Теперь величина риска по сделке составляет 12 долларов. Если проигрыш в следующей сделке сократит размер счета до 108 долларов, то сумма риска будет 10,80 доллара.

Асимметричное действие рычага устраняется так: если риск составляет 12 долларов по сделке и счет сокращается до 108 долларов, то размер риска по очередной сделке останется на уровне 12 долларов. Возьмите самую большую сумму риска и используйте ее, невзирая на уменьшение сальдо счета. Этот подход был применен при подбрасывании монеты при 10, 25 и 40% по Фиксированно-Фракционному методу, описанному ранее.

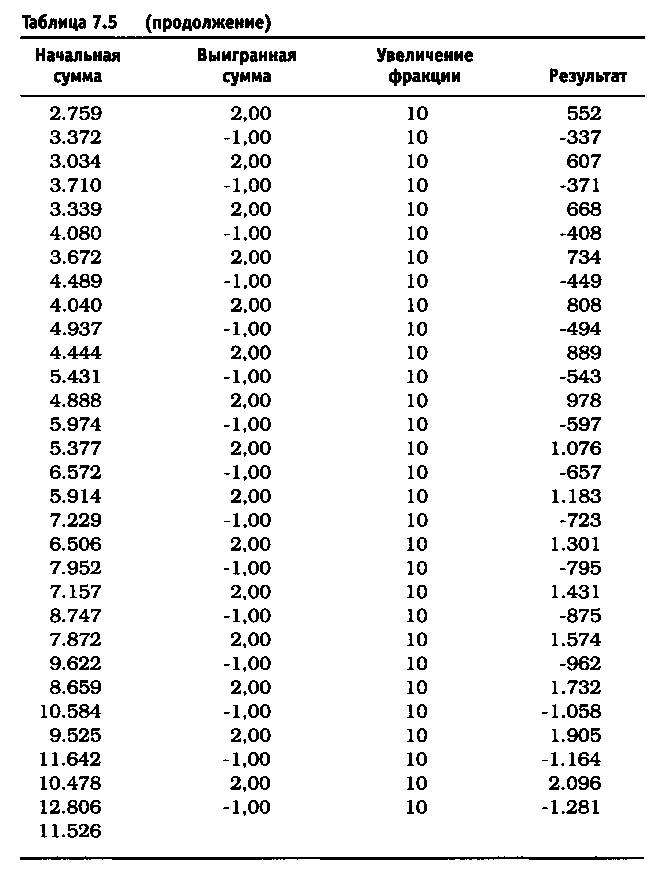
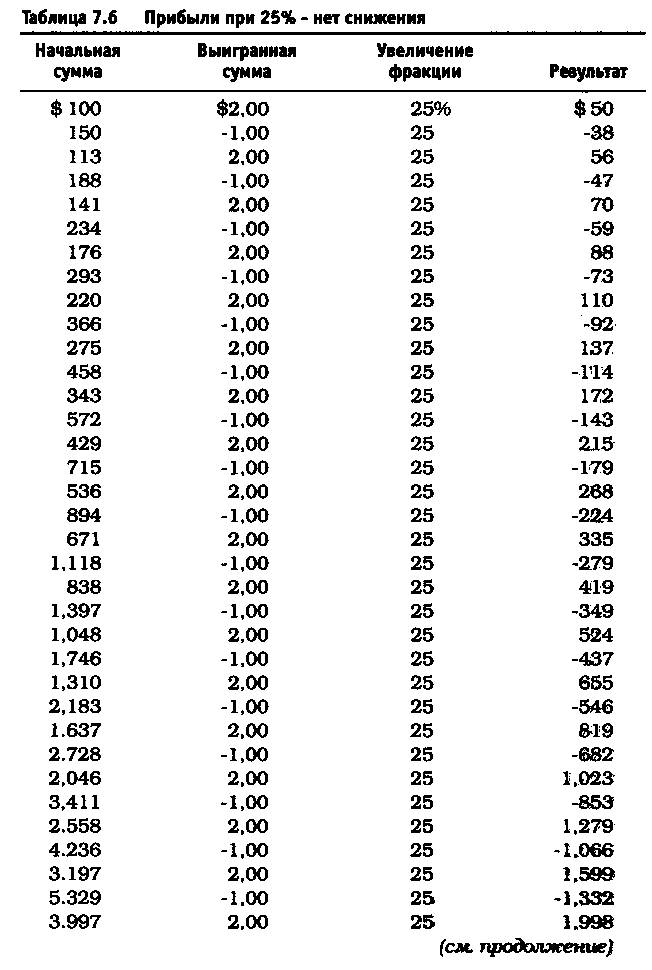
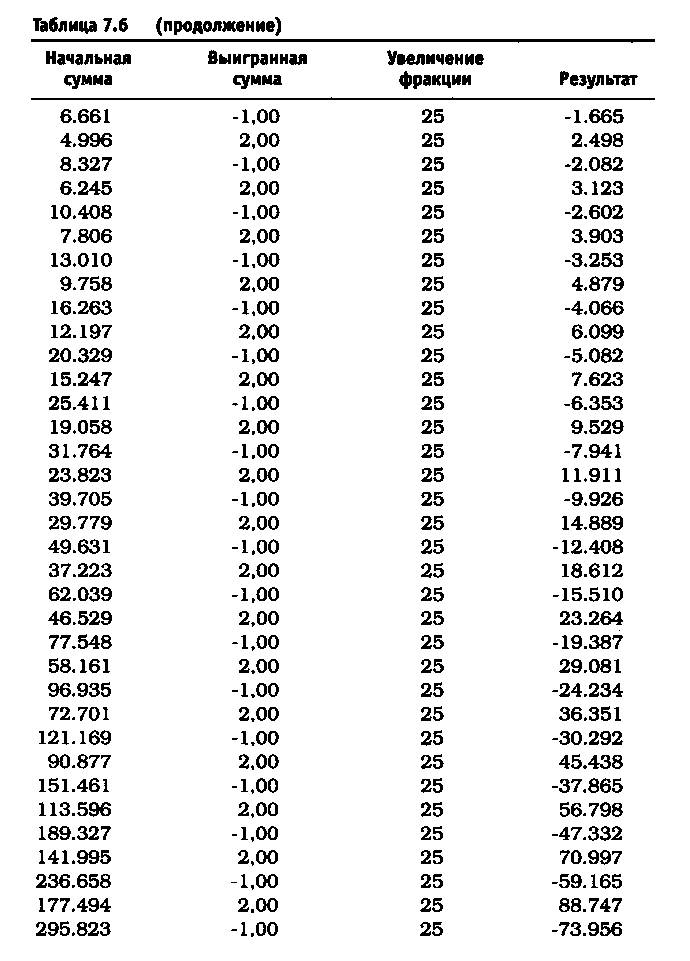
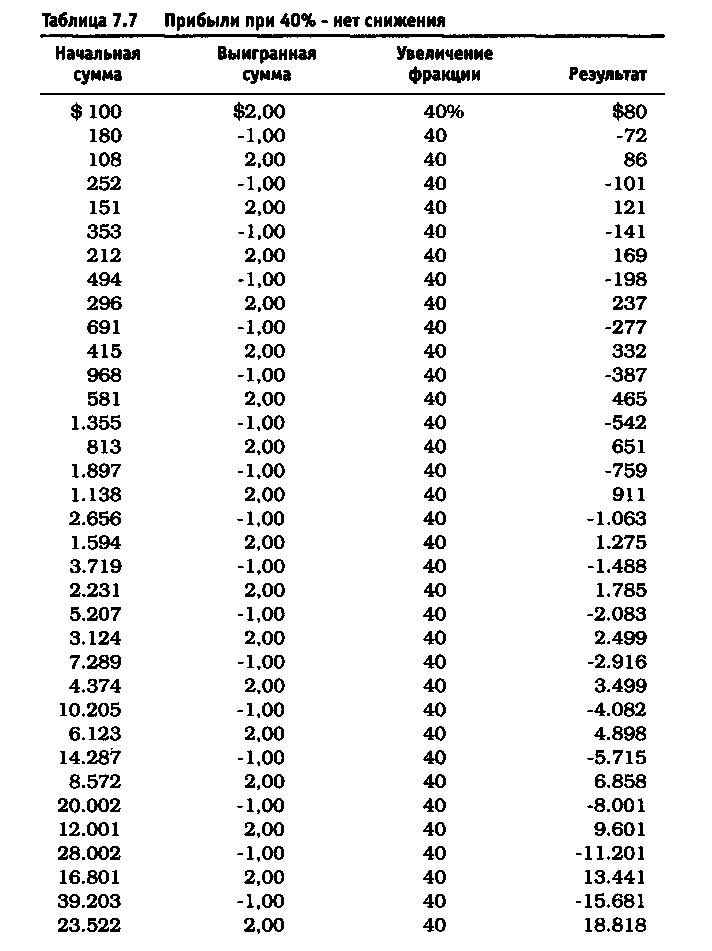
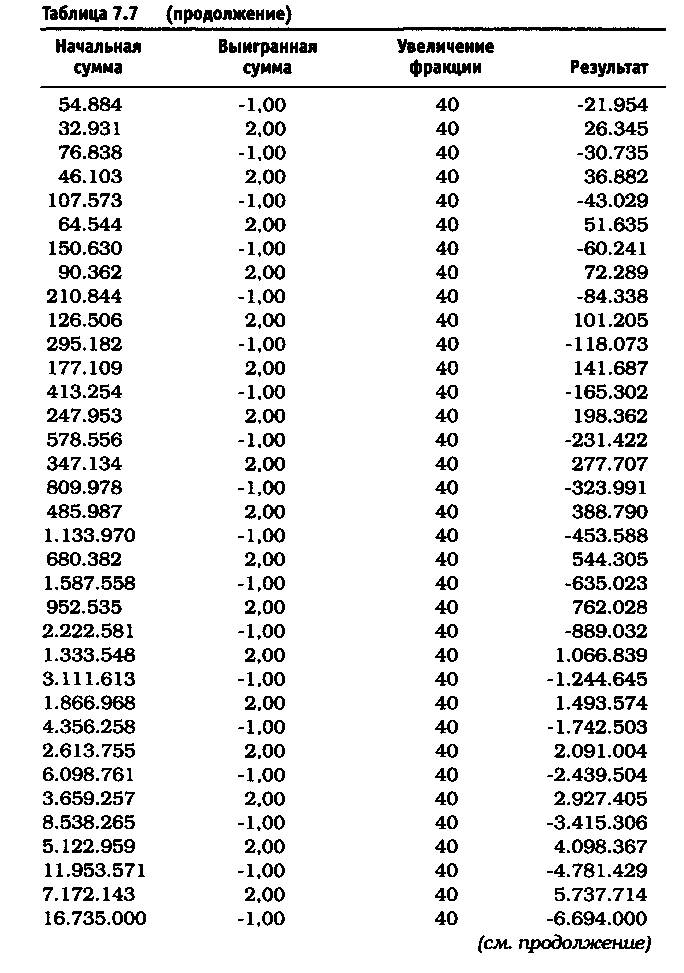
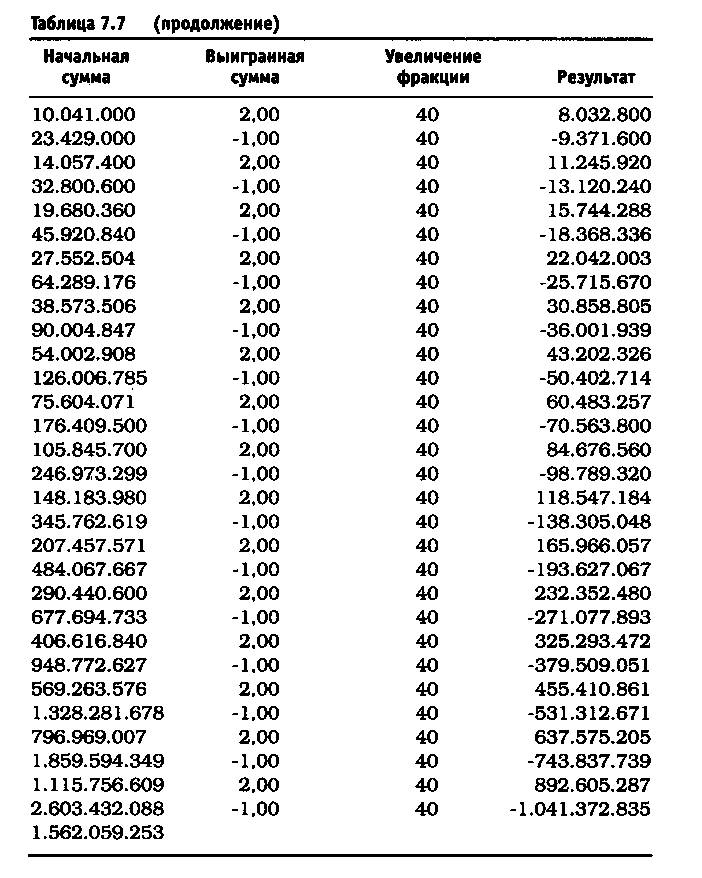
После удаления асимметричного действия рычага из уравнения реинвестирование 10% привело к росту до $11.526 долларов против $4.700 (см. таблицу 7.5). Риск в размере 25% по каждой сделке без снижения этого значения привел к тому, что оцениваемая величина возросла до $6.305.843 по сравнению с $36.100 (см. таблицу 7.6). Обратите внимание, что результаты работы не описываются гауссовой кривой, характерной для асимметричного действия рычага. При 40% прибыль получается не ниже, чем при 25%, и составляет 1.562.059.253 доллара (см. таблицу 7.7). Таков потенциал возможностей управления капиталом после устранения асимметричного эффекта рычага. Однако здесь есть одна ловушка. Эти результаты действительны при условии, что за каждым проигрышем следует выигрыш, а за каждым выигрышем — проигрыш. Используя этот метод и рискуя 25% от размера счета, через четыре проигрыша подряд вы будете вынуждены ликвидировать счет. Две потери подряд при риске в 40 долларов (или 40% от первоначальной суммы капитала) сделают невозможным придерживаться ставки пари в 40 долларов при третьем подбрасывании монеты, поскольку у вас на счете останется только 20 долларов. Этот пример — лишь схематичная иллюстрация и не более того.

Тем не менее есть возможность реализовать определенный вариант этой модели в реальной, но только не в Фиксированно-Фракционной торговле. Если при использовании Фиксированно-Фракционного метода с учетом асимметричного эффекта рычага убытки велики, то без учета этого эффекта они становятся просто огромными. Торговля из расчета нормы риска в 10% может свести счет к нулю после 10 убыточных сделок подряд. Причем задолго до перевода дополнительных средств, необходимых для поддержания маржи.

Вместе с тем, применяя эту торговую модель к Фиксированно-Пропорциональному методу, можно получить совершенно другую картину. Вспомните, что между убытками, числом контрактов, вводимых в торговлю, и дельтой существует следующее соотношение:

Ожидаемые потери на контракт =$10.000

Дельта =$5.000

Число торгуемых контрактов =10

Число контрактов может сократиться не более чем на два. $10000/$5.000 =2 10-2 =8

Вообще-то говоря, если сумма счета составляет 250.000 долларов и в торговле занято 10 контрактов, то 10 убыточных сделок подряд сократят размер счета до 159.000 долларов. Если бы риск не регулировался при возникновении убытков, то величина счета уменьшилась бы до 150.000, а не до 159.000 долларов. Поэтому риск увеличивается только на 9.000 долларов. Общие потери составили бы 40, а не 36,4%. 10 выигрышных сделок подряд на общую сумму 10.000 долларов вернут размер счета к 250.000 долларов без асимметричного действия рычага. При асимметричном действии рычага размер счета был бы равен 248.000 долларов. Поэтому в случае применения консервативных фиксированных пропорций асимметричное действие рычага имеет значительно меньший эффект.