Тема 27 Задача о назначении в управлении цепями поставок мелкопартионных грузов

Тема 27

Задача о назначении в управлении цепями поставок мелкопартионных грузов

Теоретические пояснения к решению задачи

Задачи маршрутизации перевозок мелкопартионных грузов и соответствующие им модели достаточно подробно исследованы в специальной литературе и реализованы во многих популярных автоматизированных информационных системах (АИС) для логистики, таких как «Деловая карта» (разработчик – ООО Фир ма «ИНГИТ»), Top Route (разработчик – компания Top Plan), Arc Logistics Route (разработчик – ESRI, Inc. (США)).

Одной из основных проблем при решении данных задач является их большая размерность, вызванная тем, что маршруты необходимо прокладывать между десятками и даже сотнями грузополучателей ежедневно. Второй не менее важной проблемой является необходимость выполнения жестких требований клиентов относительно времени доставки груза.

Например, при перевозке молочных продуктов все грузополучатели могут требовать доставки товара до десяти часов утра, что может вызвать затруднение в объединении в один маршрут нескольких клиентов. Следствием этого является необходимость привлечения к перевозкам дополнительного подвижного состава при его неполной загрузке и, соответственно, увеличение транспортных затрат. Третьей проблемой является существенная неравномерность поставок по дням недели и месяцам года, вызванная колебаниями спроса.

В практике работы дистрибьюторских компаний, осуществляющих доставку мелкопартионных грузов клиентам, нередко используется арендованный подвижной состав. Стоимость аренды, как правило, зависит от грузоподъемности автомобиля и сектора развозки груза. Поскольку секторы развозки формируются по территориальному принципу, то косвенно стоимость аренды зависит и от пробега автомобиля на маршруте. В данном случае минимизация общих транспортных расходов будет заключаться в оптимальной загрузке подвижного состава, вследствие чего минимизируется общее количество задействованных в перевозке автомобилей. Поскольку, как правило, при формировании развозочных маршрутов накладываются жесткие ограничения по времени доставки товаров потребителям, необходимо проверить выполнимость сформированных маршрутов.

Данную задачу можно решить с использованием дешевых и доступных любому пользователю геоинформационных систем (ГИС), включающих автоматический прокладчик маршрутов. К примеру, в г. Санкт-Петербурге эта задача решается с помощью программы «Электронный атлас автодорог. Улицы Санкт-Петербурга 2003» (фирмы «ИНГИТ») или компакт-диска «Автокарты / каталог 2004» (компании TopPlan).

Эвристические алгоритмы решения задачи формирования развозочных маршрутов включают два этапа, во-первых, группировку пунктов по маршрутам, во-вторых, определение рационального порядка объезда пунктов. Задачу группировки пунктов по маршрутам можно решить как частный случай задачи о назначениях. Ниже рассматривается алгоритм решения данной задачи и пример его практического использования.

Предположим, что имеется п грузополучателей или клиентов, каждого из которых может обслужить любой из m привлеченных для перевозок автомобилей. Стоимость обслуживания i-го клиента j-м автомобилем с или теневая цена (это цена резервирования провозных возможностей, ее величина отражает максимальную цену, которую можно согласиться заплатить за обслуживание i-го клиента), рассчитывается следующим образом:

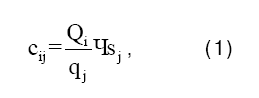
где Q_i – вес партии товара, доставленной i-му клиенту (кг); q_j – грузоподъемность j-го автомобиля с учетом класса груза (кг); s_j – затраты на рейс, выполненный j-м автомобилем (руб.).

Необходимо распределить автомобили по клиентам так, чтобы минимизировать суммарные затраты, связанные с выполнением перевозки.

В исследовании операций задача, сформулированная выше, известна как задача о назначениях. Введем переменные х_Р принимающие значение 1 в случае, когда i-го клиента обслуживает j-й автомобиль, и значение 0 во всех остальных случаях.

Тогда ограничение

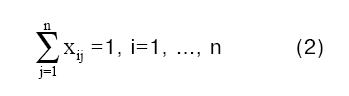
гарантирует обслуживание i-го клиента лишь одним автомобилем, то есть заказы клиентов разбивать нельзя, а ограничение

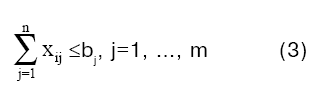
гарантирует, что каждый автомобиль будет обслуживать не более b клиентов. Это означает, что мы пытаемся учесть ограничения по времени обслуживания клиентов еще на этапе решения задачи о назначениях.

Поскольку речь идет о формировании развозочных маршрутов, необходимо учесть ограничения по грузоподъемности:

означающие, что фактическая нагрузка подвижного состава не должна превышать его грузоподъемности.

Стоимость решения, то есть сумма теневых цен для обслуженных клиентов, должна быть минимизирована. Таким образом, задачу о назначениях подвижного состава можно записать следующим образом.

Задача о назначениях является частным случаем классической транспортной задачи. При этом условие

х_ij..О{0,1}, i=1, …, m, j=1, …, n

означает выполнение требования двоичности переменных х.., то есть в допустимом целеисчислении значениями переменных могут быть только 0 и 1. Следовательно, для ее решения может быть использован эффективный вычислительный алгоритм симплексного метода, реализованный в средстве «Поиск решения» Microsoft Excel.

Данный текст является ознакомительным фрагментом.