6.2. Экономико-математическое моделирование процессов увеличения потенциала научно-производственного предприятия на основе обновления производства

6.2. Экономико-математическое моделирование процессов увеличения потенциала научно-производственного предприятия на основе обновления производства

Обновление производства предполагает использование научно-производственным предприятием совокупности технологических инноваций. В этом случае происходит модернизация основных производственных фондов предприятия, изменение выпускаемой продукции в пределах сложившейся специализации производства.

При постановке задачи обновления производства предполагается, что в процессе маркетинговых исследований отобрана номенклатура продукции, которая может быть востребована на рынке. Реализация на рынке этой продукции должна приносить предприятию максимальную прибыль. Первой группой переменных в модели является номенклатура продукции и объемы выпуска по каждой позиции номенклатуры. Для каждой позиции номенклатуры рассчитывается возможная цена реализации продукции на момент начала выпуска, а также составляется прогноз реализации от объема выпуска продукции. Модель позволяет сформировать оптимальную программу производства продукции по сформулированным критериям и не предполагает, что в окончательный план производства войдут изделия всех наименований.

Оптимальная программа производства может не соответствовать существующей структуре технологического оборудования НПП. Тогда возникает необходимость проектирования новых организационно-производственных структур с учетом возможности приобретения нового оборудования и ликвидации старого. Использование в созданных структурах технологических инноваций приводит к появлению организационно-управленческих инноваций, предполагающих применение новых методов организации производства и труда.

При обновлении производства у предприятия могут появиться избыточные площади, которые можно продать или сдать в аренду. Полученные при этом доходы станут источником финансирования процессов обновления производства. Недостающие площади предприятие может построить, купить или арендовать. Два первых способа требуют дополнительных инвестиций, которые учитываются как капитальные вложения. Арендная плата включается в себестоимость продукции предприятия.

Современные тенденции развития высокотехнологичных производств связаны с повышением уровня автоматизации производственных систем. Поэтому в модели учитывается возможность различного уровня автоматизации как укрупненных групп технологического оборудования, так и различных элементов группы. При моделировании процессов обновления производства необходима зависимость производительности каждой группы оборудования при заданном уровне автоматизации по отношению к различным предметам труда. Это важно, поскольку повышение уровня автоматизации может быть эффективно только для некоторых предметов труда, а для остальных спровоцирует резкий рост затрат на их производство.

Высокотехнологичное производство также характеризуется высоким уровнем применяемости элементов в различных моделях выпускаемой продукции. Выбор номенклатуры продукции с высокой степенью применяемости элементов повышает специализацию организационно-производственных структур НПП. Это дает возможность автоматизировать производственный процесс, снизить капитальные и текущие затраты. Поэтому на модельном уровне номенклатуру производимой продукции следует представлять не только изделиями в целом, но и составляющими их элементами – заготовками, деталями и сборочными единицами.

Сходство технологических процессов обработки однотипных элементов продукции легко представить общепринятыми методами конструкторско-технологического группирования. Таким образом, на модельном уровне любой тип продукции предприятия можно представить в виде совокупности групповых представителей его элементов и сформулировать баланс производственной мощности предприятия в терминах трудоемкости изготовления этих представителей.

В экономико-математической модели обновления производства учтена возможность существования различного уровня автоматизации внутри одной и той же группы оборудования. Это позволяет изготавливать продукцию с помощью различных вариантов технологических процессов. Различия возможны не только в уровне автоматизации выполнения некоторых операций, но и в составе, а также в последовательности выполнения операций. При разработке модели сделано предположение, что все элементы одной и той же группы продукции обрабатываются по одной и той же технологии, которая является наиболее эффективной из всех допустимых.

Последней группой переменных экономико-математической модели являются суммарные инвестиции в оборудование и производственные площади, а также количество технологического оборудования и размер дополнительных или избыточных производственных площадей. Модель базируется на предположении, что величина дополнительных капитальных вложений ограничена и зависит от внешних факторов по отношению к модели.

Критерием оптимальности модели является максимум чистого дисконтированного дохода. При его расчете инвестиционные затраты рассматриваются как капитальные вложения в создание технологических инноваций, производственных площадей и организационно-производственных структур за вычетом стоимости оборудования и производственной площади, подлежащих ликвидации.

Затраты предприятия по созданию технологической инновации включают в себя расходы на выполнение научно-исследовательских работ, создание конструкторско-технологической документации и правовую охрану созданной интеллектуальной собственности. Капитальные вложения в создание организационно-производственных структур включают затраты на производственные и служебно-бытовые площади, оборудование, технологическую оснастку и специальные приспособления, а также учитывают оборотные средства в незавершенном производстве.

Ограничения в экономико-математической модели обновления производства распространяются на объем реализации продукции, фонды времени используемого оборудования, объем инвестиций. Кроме того, экономико-математическая модель содержит ограничение на допустимое использование производственной площади.

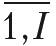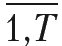Вид изделий, потенциально допустимых к выпуску, в модели обозначен индексом i, а объем выпуска i-го изделия в году t-индексом х_it (i = ; t = ). Прямые материальные затраты на выпуск единицы i-го изделия для каждого t-го года составляют величину m_i. Состав i-го изделия в модели представлен совокупностью деталей различных групп. Группа элементов обозначена индексом g (g = 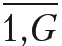), а коэффициент применяемости элементов группы g в i-м изделии – символом 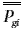. Причем величина P_gi не меняется в течение периода T.

Для формализации зависимости цены реализации i-го изделия от объема его выпуска введено понятие интервала объема выпуска. Предполагается, что при изменении объема выпуска внутри этого интервала рыночная цена изделия не изменяется. Нижняя и верхняя границы интервала объема выпуска x_it обозначены b^H_it и B^B_it

Каждому интервалу объема выпуска x_it соответствует цена реализации C_i. В модели используется булева переменная V_it, принимающая значение:

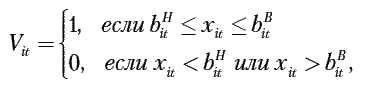
т. е. переменная V_it равна 1, если объем выпуска i-го изделия попадает в соответствующий интервал i_n, и равна 0 – в противном случае.

Индекс j обозначает номер группы технологического оборудования (j = 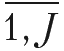). Элементом j-й группы может быть рабочее место или производственный модуль, в том числе полностью или частично автоматизированный производственный комплекс, сборочный стенд или сборочная линия, выполняющая операции определенного типа. Индекс j_r в экономико-математической модели означает r-й уровень автоматизации элемента j-й группы технологического оборудования, а R_j – количество допустимых уровней автоматизации в j-й группе.

Варианту технологического процесса обработки представителя g-й группы элементов в экономико-математической модели соответствует индекс k (k = 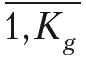). Эти варианты могут различаться составом и степенью автоматизации различных операций. Таким образом, любое изменение технологии выполнения операции приводит не к изменению описания отдельной операции, а к появлению нового варианта технологического процесса. В экономико-математической модели порядок операций не играет существенной роли. Поэтому при описании операции ей соответствуют индексы группы оборудования, уровня автоматизации и номер варианта технологического процесса, к которому эта операция относится. В модели ?^k_gjr характеризует фондоемкость обработки представителя g-й группы элементов на j-й группе оборудования при r-м уровне автоматизации по k-му варианту технологического процесса, а Z^k_gjr – себестоимость выполнения той же операции. В модели величины ?^k_gjr и Z^k_gjr не зависят от t.

Через f_jrt в модели обозначен располагаемый фонд времени элемента оборудования j-й группы, имеющего r-й уровень автоматизации. Искомое количество того же оборудования в году t составит y_jrt, наличное – Y_jrt. В модель вводится булева переменная ?_jrt. Она принимает значение 1, если y_jrt ? Y_jrt, и 0 – в противном случае. Себестоимость машино-часа эксплуатации технологического оборудования j-й группы, имеющего r-й уровень автоматизации, обозначена величиной d_jr.

Капитальные вложения в создание одного элемента j-й группы технологического оборудования, имеющего r-й уровень автоматизации для года t, обозначаются q_jrt. Они не включают вложения в создание, приобретение или аренду производственной площади, необходимой для размещения данного элемента оборудования. Ожидаемая цена реализации оборудования j-й группы, имеющего r-й уровень автоматизации в году t, составляет ?_jrt.

Производственная площадь, занимаемая одним элементом j-й группы технологического оборудования, имеющего r-й уровень автоматизации, составляет s_jr, искомая величина производственной площади – S, располагаемая величина – Р. В модель введена булева переменная ?, принимающая значение 1 при S > Р и 0 – в противном случае. Капитальные вложения в создание 1 м² дополнительной производственной площади составляют ?, годовые затраты на аренду – П, а текущие годовые затраты на содержание и эксплуатацию 1 м² производственной площади – ?.

Общими параметрами модели являются инвестиции научно-производственного предприятия в разработку или приобретение технологической инновации в году t(К^ТИ_t), суммарные дополнительные капитальные вложения в производство (К), максимально допустимая величина привлечения капитальных вложений со стороны (Q), годовая норма дисконта (Е), годовая норма платы за пользование капитальными вложениями со стороны (?).

Предполагается, что величина нормы дисконта одинакова по отношению к капитальным вложениям, финансируемым предприятием за счет собственных средств и средств, привлеченных со стороны. Такое предположение верно, поскольку необходимо обеспечить эффективность обновления производства по отношению к любым источникам финансирования. В противном случае показатель рентабельности капитальных вложений не будет отражать потребности предприятия в обновлении производства на будущие периоды.

Ограничения модели имеют следующий вид:

1. По объему реализации продукции:

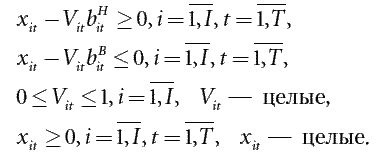
2. По фондам времени групп оборудования:

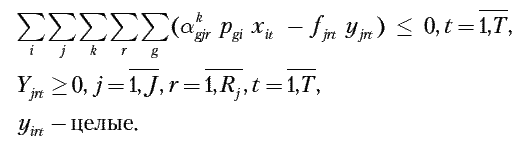
3. По производственной площади:

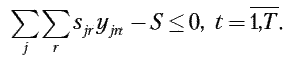
4. По объему дополнительных капитальных вложений:

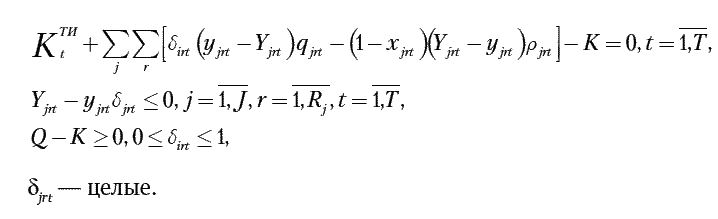
Последнее ограничение не учитывает возможности приобретения или строительства предприятием недостающей производственной площади. Рассмотрение таких вариантов на модельном уровне затруднительно. Это связано с тем, что ошибочно относить соответствующие капитальные вложения предприятия только на рассматриваемую годовую программу выпуска продукции. Такие решения принимаются административным путем. При отсутствии у предприятия источников финансирования потребность в капитальных вложениях на расширение производственных площадей можно учесть путем уменьшения величины суммарных дополнительных капитальных вложений в производство.

Критерий оптимальности удобнее рассмотреть по частям. В себестоимости продукции прямые материальные затраты в расчете на годовой выпуск продукции составят величину m_ix_i, а текущие затраты на содержание и эксплуатацию оборудования в t-м году равны

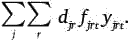
Текущие затраты предприятия на содержание и эксплуатацию существующей и арендуемой производственной площади, а также затраты на возможную аренду составят S? + ?(S – P)П, плата за пользование предприятием заемными средствами составит eQ.

Капитальные вложения в t-м году (без учета оборотных средств) в обновление производства составят

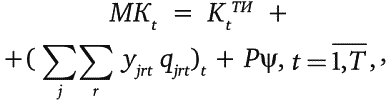
а за весь срок реализации проекта обновления производства равны

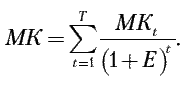
Тогда целевая функция эффективности примет следующий вид:

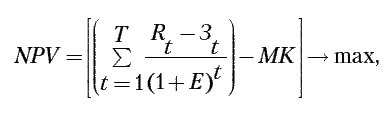
где R_t и З_t – стоимостная оценка результатов и текущих затрат в t-м году реализации проекта обновления производства.

Экономическая оценка результатов в t-м году составит

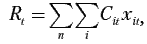
а текущих затрат:

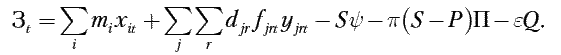
Величина, определяющая разность результатов и затрат для t-го года в критерии оптимальности, рассчитывается по формуле:

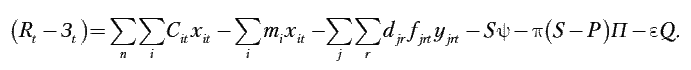
В полученной модели особый интерес представляет компактность формулировки критерия оптимальности. Достигнуто это благодаря тому, что текущие затраты на содержание и эксплуатацию оборудования, бытовых помещений, а также заработную плату отнесены к стоимости машино-часа содержания и эксплуатации единицы оборудования. Исключение составляют текущие затраты на содержание и эксплуатацию производственных помещений. Такое исключение является объективно необходимым. Это связано с тем, что оплата аренды производственных помещений по своему экономическому смыслу отличается от затрат на содержание и эксплуатацию собственных площадей предприятия.

Полученная экономико-математическая модель является частично целочисленной, поскольку в ней используются непрерывные и целочисленные переменные, а ограничения и критерий оптимальности имеют нелинейный вид. Поэтому реальное решение задачи обновления производства с помощью предлагаемой модели затруднительно. Однако полученная экономико-математическая модель полезна в качестве компактного описания взаимодействия факторов, влияющих на принятие оптимального решения.

В то же время при решении конкретных задач, возникающих на стадии обновления производства, уровень неопределенности исходных данных практически всегда гораздо ниже, чем предусмотрено формулировкой решаемой задачи. В конкретной ситуации всегда известно, работает НПП на свободный рынок или существует совокупность предложенных предприятию заказов с заранее оговоренной ценой.

В других случаях предприятие уже знает и зафиксировало предполагаемый уровень автоматизации различных групп оборудования. Например, в условиях избыточности рынка труда уровень автоматизации следует принимать как минимальное значение, при котором обеспечивается конкурентоспособность продукции предприятия. Это обусловлено тем, что затраты на возмещение капитальных вложений и текущих затрат, связанных с автоматизацией, не будут окупаться вследствие достаточно низкой заработной платы работников. При тех же условиях аренда производственных помещений, как правило, становится для предприятия экономически нецелесообразной. Поэтому необходимо рассмотреть упрощенные модификации модели для конкретных условий обновления производства.

При заданной программе выпуска продукции в экономико-математической модели из рассмотрения исключаются переменные x_it. Тогда ограничение 1 приобретает следующий вид:

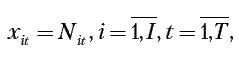
где N_it – заданный объем выпуска i-го изделия в году t.

Автоматически во всех остальных ограничениях величины x_it будут заменены на N_it. Ограничение по фондам времени используемых групп технологического оборудования не изменит своего вида с точностью до замены x_it на N_it. Ограничения по производственной площади, объему дополнительных капитальных вложений не изменятся.

Критерий оптимальности изменится незначительно – выручка от реализации продукции в критерии оптимальности станет заданной постоянной величиной. Поэтому существенных изменений в характере экономико-математической модели, а также в возможностях ее численной реализации не произойдет.

При заданном уровне автоматизации модель должна учитывать два варианта функционирования НПП: в условиях рыночной реализации продукции и работы предприятия на заказ. В первом случае ограничения экономико-математической модели и целевая функция будут иметь следующий вид:

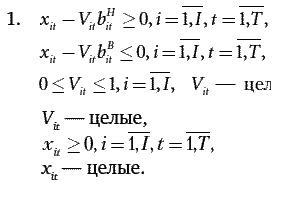
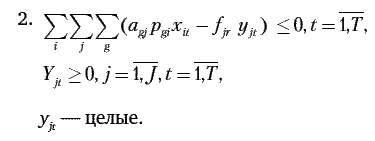
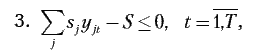
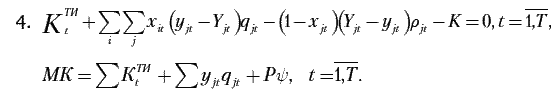
Тогда величина, определяющая разность результатов и затрат для t-го года в критерии оптимальности, рассчитывается по следующей формуле:

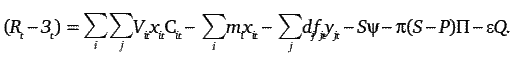
Во втором случае в экономико-математической модели из рассмотрения исключаются величины b^H_it и b^B_it, а x_it=N_it, i = 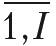, t = 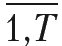. Остальные ограничения сохранят предыдущий вид. Величина, определяющая разность между результатами и затратами для t-го года в критерии оптимальности, может быть записана следующим образом:

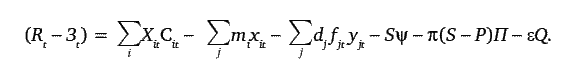
Рассмотренные варианты упрощений существенно не отличаются от первоначального варианта модели с точки зрения перспектив реализации. Все варианты упрощений модели остаются смешанными и нелинейными, не облегчая нахождения численного решения. Поэтому целесообразно рассмотреть максимально допустимые упрощения первоначально полученной экономико-математической модели.

Допустим, что ориентировочно известны интервал объема выпуска продукции по каждой позиции номенклатуры и соответствующая цена. Обозначим нижнюю границу интервала значений объема выпуска i-го изделия символом n_i, а верхнюю – N_i. Тогда ограничение 1 в модели будет иметь следующий вид: x_i ? n_i,, x_i < N_i, i = 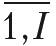. Такое преобразование переводит ограничение 1 в линейную область.

Аналогично преобразуется к линейному виду ограничение 2. Зафиксируем технологический процесс обработки деталей g-й группы. Тогда автоматически фиксируется и уровень автоматизации r используемого в этом технологическом процессе оборудования. Такая фиксация не означает, что все технологическое оборудование j-й группы будет иметь один и тот же уровень автоматизации. Напротив, разбиение технологического оборудования на группы станет более мелким, а понятие группы оборудования приобретет большую детализацию. Это означает, что элементы j-й группы технологического оборудования с разным уровнем автоматизации будут теперь относиться к разным группам оборудования. Таким образом, индексы k и r в модели из рассмотрения исключаются, а ограничение 2 примет следующий вид:

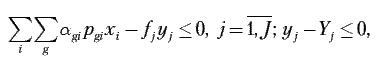
где ?_gj – трудоемкость обработки деталей – представителей g-й группы на j-й группе технологического оборудования в новой трактовке этой группы.

Переменная y_j во вновь сформулированном ограничении приобретает новый смысл. Она будет означать не искомое количество технологического оборудования j-й группы для выполнения программы производства, а используемое количество оборудования этой группы. При этом величина y_j заранее ограничивается наличным или допустимым к использованию количеством оборудования в данной группе Y_j.

Ограничение 3 по производственной площади приобретет смысл определения потребности предприятия в производственной площади, необходимой для размещения используемого технологического оборудования, и будет иметь следующий вид:

?_js_j y_j – S = 0.

Привести ограничение 4 к линейному виду невозможно. Если исключить булеву переменную ?_jr под знаком ?, то это приведет к неоправданному сложению затрат на расширение j-й группы технологического оборудования и «экономии» на уменьшении ее состава. Причем обе эти величины будут рассчитаны по цене покупки. Аналогично второй элемент суммы будет учитывать те же затраты, только с обратным знаком по цене реализации излишков оборудования предприятия. Такой подход искажает реальную ситуацию. Исключение ограничения 4 из модели означает, что активная часть производственных фондов не преобразуется в процессе обновления производства.

Допустив, что активная часть производственных фондов предприятия не изменяется, мы расширили номенклатуру производимой продукции. В этом случае вопрос о дополнительных капитальных вложениях из рассмотрения также исключается. При этом проблемы о возможном расширении производственных площадей и о дополнительных капитальных вложениях решаются административными методами. Соответственно, в модели критерий оптимальности приобретет следующий вид:

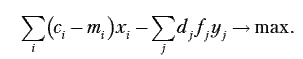
где d_j – затраты в расчете на один машино-час содержания и эксплуатации оборудования j-й группы;

f_j – годовой фонд времени работы единицы оборудования j-й группы.

Анализируя полученный критерий оптимальности, можно заметить, что по отношению к первоначальному виду он изменился не только по форме, но и по содержанию. Теперь вместо максимума чистого дисконтированного дохода требуется обеспечить максимум прибыли предприятия. Такая трансформация критерия оптимальности естественна, если учесть, что объем капитальных вложений был зафиксирован путем исключения из рассмотрения ограничения 4 по объему дополнительных капитальных вложений. Тогда окончательно упрощенная экономико-математическая модель будет иметь следующий вид.

Ограничениями экономико-математической модели являются:

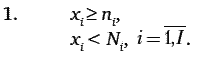
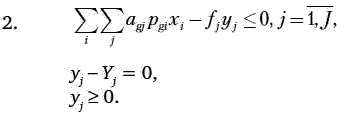
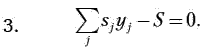
Критерий оптимальности экономико-математической модели:

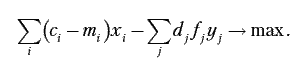
В такой записи экономико-математическая модель обновления производства становится линейной. Добавив к этой модели требование xi, yj – целые, для решения можно использовать существующие алгоритмы целочисленного программирования.

При приведении модели обновления производства к реализуемому виду из нее были исключены факторы, ограничивающие дополнительные капитальные вложения, а также затраты на использование привлеченного со стороны капитала и его возмещение. В окончательном виде экономико-математическая модель представляет собой модель баланса производственных ресурсов предприятия. С использованием методов планирования эксперимента эта модель может быть применена на практике для решения конкретных задач формирования конкурентной стратегии предприятия.

Данный текст является ознакомительным фрагментом.