Нормальное распределение: тайна колоколообразной кривой

Нормальное распределение: тайна колоколообразной кривой

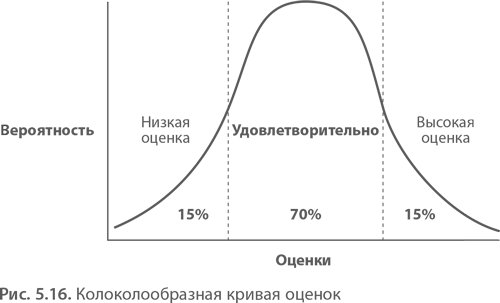
Нормальное распределение встречается чаще всего, а его графическое представление обычно называют колоколообразной кривой. В Гарварде при выставлении оценок используют колоколообразную кривую. Кривая показывает, что 15 % слушателей получают низкую оценку (проходной балл). В Дарденской бизнес-школе преподаватели ставят неудовлетворительную оценку, основываясь на собственном суждении. Результат: в двух кампусах сложилась принципиально разная конкурентная среда.

Когда вероятностная мера выводится на основании множества проб, точки кривой сближаются, и она принимает колоколообразные очертания. Такую кривую мы называем функцией плотности вероятности. Именно так выглядели графики осадков в Сиэтле. Горб посреди кривой объясняется центральной предельной теоремой. Она гласит, что «распределение средних арифметических для повторяющихся независимых выборок принимает форму колоколообразного нормального распределения». Почему? Просто потому, что при большом числе независимых выборок итог стремится к центральному среднему арифметическому.

Концепция «средних по выборкам» довольно расплывчата. На практике речь идет о достаточно больших группах данных. Почему? Потому что нормальное распределение легко использовать, и оно всегда оказывается близко к реальности. Курс акций – это отражение многочисленных конъюнктурных колебаний на рынке, результатом которых будет благоприятный или неблагоприятный исход. Этот результат можно рассматривать в качестве «среднего арифметического» конъюнктурных колебаний. Едва ли не все происходящее можно рационализировать через среднее арифметическое, и этим объясняется полезность нормальных распределений.

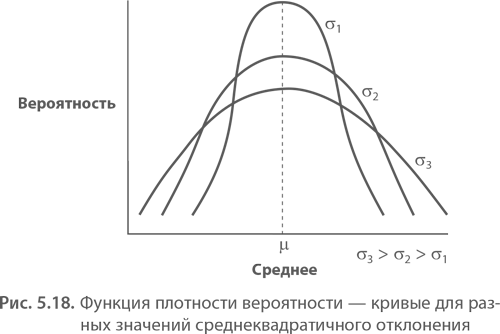
Параметры нормальной кривой. Колоколообразная кривая характеризуется двумя параметрами: средним и стандартным (среднеквадратичным) отклонением (СКО). Среднее (?) является центром кривой. Обычно его называют средним арифметическим. Оно вычисляется делением суммы значений на их количество. Среднеквадратичное отклонение (?) определяет ширину кривой. СКО можно также описать как критерий «отклонения от среднего». Две эти характеристики играют ключевую роль в большей части концепций теории вероятности.

Другие критерии средней величины для совокупности данных – медиана, величина, стоящая в середине упорядоченного по возрастанию списка данных, и мода – величина, чаще всего встречающаяся в выборке.

Как и в случае биномиального распределения, сумма всех исходов, представленная площадью под кривой, равна 100 %. Особенность нормальной кривой заключается в том, что для любого среднеквадратичного отклонения от среднего или центра вероятность события одинакова, независимо от формы кривой.

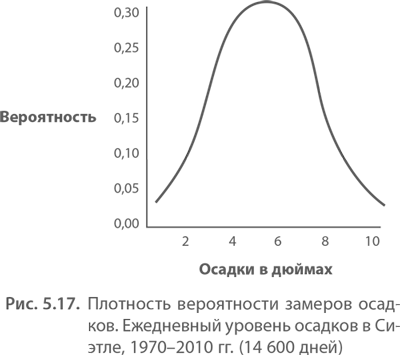
Пример нормального распределения из розничной торговли. Эл Банди, владелец обувного магазина, хочет быть уверен, что на складе имеются запасы обуви любого размера. Он купил в Академии ног данные по частоте женских ног и получил результаты проведенного Академией опроса.

На миллиметровке Банди расположил эти данные и получил нормальное распределение. Он также ввел данные в свой калькулятор и нажал кнопку «стандартное отклонение». Ответ был «2». Эл также проверил среднее арифметическое для всей совокупности ответов по размерам и получил ответ «7». Посмотрев на кривую, он увидел внушающее доверие нормальное распределение (рис. 5.17).

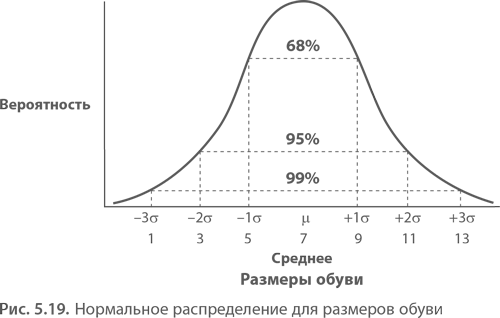
Как только Эл распознал кривую, он смог применить законы нормального распределения. Площадь участков под нормальной кривой всегда описывается формулой:

1 СКО = 0,3413

2 СКО = 0,4772

3 СКО = 0,49865

4 СКО = 0,4999683

Если мистер Банди, учтя эти данные, запасет размеры с 5-го по 9-й, он сможет удовлетворить потребности 68,26 % (0,3413 ? 2) покупательниц. Расширив ассортимент склада с 3-го по 11-й размеры, он сможет обуть 95,44 % женщин. Если же Эл будет иметь на складе размеры с 1-го по 13-й, 99,73 % клиентов уйдут от него с покупкой. Для тех, у кого размер меньше 1-го или больше 13-го, он может сделать специальный заказ.

Естественно, таблицы нормальных распределений составлены для определения вероятности любой конкретной точки на кривой (с учетом нецелочисленных СКО). Для пользования таблицами необходимо рассчитать значение Z.