6. 5. Системы управления запасами

6. 5. Системы управления запасами

Учитывая значение запасов, исследование логистической системы должно строиться на следующих вопросах:

• какой уровень запасов необходимо иметь для обеспечения требуемого уровня обслуживания потребителя;

• в чем состоит компромисс между уровнем обслуживания потребителя и уровнем запасов в системе логистики;

• какие объемы запасов должны быть созданы на каждой стадии производственного процесса;

• должны ли товары отгружаться непосредственно с предприятия;

• каково значение компромисса между выбранным способом транспортировки и запасами;

• каковы общие уровни запасов на данном предприятии, связанные со специфическим уровнем обслуживания;

• как меняются затраты на содержание запасов в зависимости от изменения количества складов;

• как и где следует размещать страховые запасы?

Логистическая система управления запасами проектируется с целью непрерывного обеспечения потребителя каким-либо видом материального ресурса. Реализация этой цели достигается выполнением таких задач, как:

• учет текущего уровня запаса на складах различных уровней;

• определение размера гарантийного (страхового) запаса;

• расчет размера заказа;

• определение интервала времени между заказами.

Для решения проблем, связанных с запасами, предназначены модели управления запасами. Модели должны отвечать на два основных вопроса: сколько заказывать продукции и когда. Есть множество разнообразных моделей, каждая из которых подходит к определенному случаю, рассмотрим четыре наиболее общих модели.

1. Модель с фиксированным уровнем запаса, работающая следующим образом: на складе есть максимальный желательный запас продукции (МЖЗ), потребность в этой продукции уменьшает ее количество на складе и как только количество достигнет порогового уровня, размещается новый заказ. Оптимальный размер заказа (ОР) выбирается таким образом, чтобы количество продукции на складе снова ровнялось МЖЗ. Так как продукция не поставляется мгновенно, то необходимо учитывать ожидаемое потребление во время поставки, поэтому следует принимать в расчет резервный запас (РЗ), служащий для предотвращения дефицита. Для определения максимального желательного запаса (МЖЗ) используется формула

МЖЗ = ОР + РЗ

2. Модель с фиксированным интервалом времени между заказами, работающая следующим образом: с заданной периодичностью размещается заказ, размер которого должен пополнить уровень запаса до МЖЗ.

3. Модель с установленной периодичностью пополнения запасов до установленного уровня, работающая по следующей схеме: заказы делаются периодически (как во второй модели), но одновременно проверяется уровень запасов. Если уровень запасов достигает порогового значения, то делается дополнительный заказ. В зафиксированные моменты заказов расчет размера заказа осуществляется по формуле

Р3 = МЖЗ – ТЗ + ОП

где РЗ – размер заказа, шт.;

МЖЗ – максимальный желательный заказ, шт.;

ТЗ – текущий заказ, шт.;

ОП – ожидаемое потребление за время.

В момент достижения порогового уровня размер заказа определяется по формуле

РЗ = МЖЗ – ПУ + ОП

где ПУ – пороговый уровень запаса, шт.

4. Модель «минимум – максимум», работающая следующим образом: контроль за уровнем запасов осуществляется периодически и если при проверке оказалось, что уровень запасов меньше или равен пороговому уровню, то делается заказ. При рассмотрении этих моделей видно, что первая модель довольно устойчива к увеличению спроса, задержке поставки, неполной поставке и занижению размера заказа. Вторая модель устойчива к сокращению спроса, ускоренной поставке, поставке завышенного объема и завышенного размера заказа. Третья модель объединяет все плюсы двух первых моделей.

Для получения ответа на вопросы: когда и сколько заказывать материалов, необходимо рассчитать объем резервного запаса и оптимального размера заказа. При расчете объема резервного запаса (РЗ) рассматриваются два случая: спрос на продукцию (П_д) – детерминированная или случайная величина. В первом случае:

РЗ = П_дT_зп

где Т_зп – время возможной задержки поставки.

Во втором случае время поставки и время возможной задержки поставки детерминированы. Значит ежедневный спрос за предыдущий период определяется как математическое ожидание М(П_д) и дисперсия Д(П_д).

Спрос за четыре и более дней распределяется по нормальному закону с математическим ожиданием

М(П_д) = QМ (П_д)

и дисперсией

Д(П_д) = QМ(П_д)

где Q – время между моментом размещения заказа и его получения

Зададимся вероятностью возможного дефицита a = 0,1.

По таблице нормального распределения находим F(Ха) = 0,9, значит,

РЗ = Xад (П_д) + М(П_д)

Таким образом, находим уровень резервного запаса из условия, что вероятность возможного дефицита будет не более заданного.

Оптимальный размер заказа находится по формуле Уилсона:

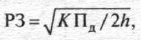
где К – затраты на размещение одного заказа;

h – издержки на хранение одной единицы продукции за одну единицу времени.

Выше рассмотрена однопродуктовая модель. В реальных ситуациях заказы делаются не на отдельные виды продукции, а на множество (с одними транспортными расходами). При переходе к многопродуктовой ситуации расчеты резервного запаса и оптимального размера заказа не меняются. Однако в этих случаях более эффективными оказываются вторая и третья модели.