Планирование

Планирование

Генри Гант и его диаграммы. В конце 1880-х гг. Генри Гант постулировал, что нормативы можно устанавливать не только на выполнение заданий, но и на планирование. «Мистер Планирование» понял, что распределение времени следует оптимизировать таким образом, чтобы эффективно планировать, координировать и выполнять производственные задания. Сбой планирования привет к появлению затыков и общей неэффективности системы.

Диаграммы Ганта, вклад Генри Ганта в решение проблемы эффективности – это таблицы, в которой задания, предусмотренные производственным циклом, отображаются вдоль одной оси, а их очередность – по другой. С помощью диаграммы Ганта можно распланировать производственный процесс в целом, выявить критические задания и узкие места. Диаграммы Ганта можно использовать в самых разных производственных системах, они ничем не привязаны к конкретным предприятиям. По сути дела, любой проект, например покупки дома, можно отобразить на сетевой диаграмме Ганта (рис. 7.2).

Планирование методом критического пути. В 1950-х гг. появился более изощренный способ оптимизации планирования: метод критического пути. Этот метод СРМ используется в сложных производственных проектах, в которых приходится координировать многочисленные задания. Еще более сложная разновидность называется методом планирования и оценки, однако сегодня эти методы рассматриваются в бизнесе как взаимозаменяемые.

Используя метод критического пути, управляющий производством располагает задания или действия в определенной последовательности и оценивает время, необходимое для выполнения каждого. Начало или завершение каждого действия называется событием. При анализе методом критического пути на схеме отображаются все события проекта. Это позволяет инженеру на производстве оценивать и регулировать время выполнения работы. На схеме показывают все задания без исключения, поэтому можно вычленить критические действия. Задания, которые могут задержать реализацию проекта, считаются критическими. Диаграмма организует во времени и выделяет критические задания, позволяя прогнозировать общую продолжительность осуществления проекта.

Возьмем для примера Кипа Мустанга, инженера-производственника компании General Dynamics, который хотел бы наладить выпуск нового переключателя для истребителей. Пилоты, участвовавшие в 2003 г. в Иракской операции, остались недовольны работой этого реле, включающего механизм катапультирования. Кип определил пять основных действий, связанных с проектом:

А: Проектирование производственного оборудования и изготовление рабочих чертежей = 2 недели.

В: Подготовка производственных помещений к размещению новых станков и запасных частей к ним = 4 недели.

С: Приобретение оснастки и комплектующих = 3 недели.

D: Создание запаса комплектующих и установка производственного оборудования = 1 неделя.

Е: Опробование новой производственной линии = 1 неделя.

Схема критического пути будет иметь следующий вид (рис. 7.3).

Каждое задание на этой схеме представлено стрелкой действия и кружком события. Согласно схеме, на кратчайшую последовательность операций при создании производственной линии потребуется 7 недель. Действия на наиболее длинном, или критическом, пути определяют продолжительность всего проекта. Когда критические задания удается выполнить быстрее, это называют ускорением проекта, так как появляется возможность досрочного его завершения. Если бы приобретение комплектующих удалось осуществить быстрее, общее время нашего проекта сократилось бы. Если любое из критических действий, например все то же приобретение оснастки, затянется, проект не будет завершен в срок. Некритические действия, такие как подготовка производственного помещения, не задерживают проект, так как для них имеется резерв времени.

В крупных инженерно-технических, строительных и производственных проектах необходимо отслеживать ход выполнения огромного числа заданий. Для таких проектов разработаны программные пакеты, помогающие строить схемы и выполнять расчеты времени. Недостатком этого замечательного инструмента являются затраты времени на создание схем критического пути и скучную работу с ними. «Сообща мы сделали их все [схемы, в 1950-х гг.], – вспоминает Дональд Фрей, директор компании Bell & Howell Co., – но потратили на это столько сил, лучше бы приложили их к работе». Ныне эти схемы выполняют на компьютере, и, хотя времени и сил они по-прежнему требуют немало, теперь с ними можно справиться.

Теория очередей в планировании. Никогда не стояли в очереди в банке? Никогда не висели на телефоне, пытаясь заказать что-либо? Если стояли и висели, тогда теория очередей, она же теория массового обслуживания, может вас заинтересовать. Очередь – это цепочка из людей или продуктов, которые ждут обслуживания. Каждого, кто обслуживает людей в очереди, называют каналом. МВА используют теорию очередей, распределяя людские ресурсы и организуя ожидание в целях экономии денежных средств и улучшения обслуживания. Проблема эффективности здесь – это определение оптимального количества каналов для обслуживания очереди. Например, управляющий банком хотел бы иметь в своем финансовом учреждении малочисленный штат служащих и короткие очереди.

Для решения проблем, связанных с очередями, нужно определить следующие данные:

А = среднее количество случайных прибытий в систему в единицу времени;

S = среднее количество операций на канал обслуживания в единицу времени;

М = количество каналов обслуживания.

Располагая этой информацией и несколькими таблицами, вы можете произвести расчеты:

Продолжим рассмотрение примера с банком. Представим себе отделение Citybank в Нижнем Манхэттене с одним работником, обрабатывающим депозиты со скоростью 50 операций в час, и средней интенсивностью прибытия клиентов 45 человек в час.

Располагая этой информацией и краткой таблицей (7.1), устанавливаем, что среднее количество людей, ожидающих в очереди, составит 8,1 человека.

Представляется вполне логичным, что, добавив второго работника, вы сможете сократить среднюю длину очереди с 8 до 4 человек. Не так ли?

Два работника, обрабатывающие депозиты:

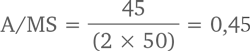
Очередь людей, ожидающих, когда их обслужат, должна с появлением второго работника уменьшиться на 97 %. При такой напряженной очереди второй работник кардинально изменяет ситуацию. Только теория очередей могла подсказать вам это. Задача с работником банка – одна из простейших. Вокруг очередей сложилась целая наука. Ученые написали книги с множеством таблиц и диаграмм для решения проблемы очереди. Вы можете не быть экспертом в данной области, но отныне знаете о существовании теории массового обслуживания. На таком принципе построены почти все курсы в программе МВА: они знакомят вас с основами, но при этом предполагается, что, став дипломированным МВА, вы сумеете найти эксперта, который реализует вашу программу.

Данный текст является ознакомительным фрагментом.