Выбор вида регрессионной модели
Неизвестную функцию f(X) в окрестностях точки, соответствующей средним уровням каждого фактора, можно представить отрезком степенного ряда. Так как интервалы варьирования факторов невелики, то можно ограничиться линейным приближением в виде множественной линейной регрессии.
Уравнение множественной линейной регрессии описывается формулой
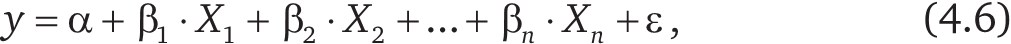
где y – зависимая переменная (отклик), рыночная стоимость 1 м2 площади объекта; Х1, Х2… Хn – независимые переменные (предикторы или факторы); ? – константа регрессии; ?1, ?2… ?n – коэффициенты регрессии; n – количество факторов сравнения; ? – случайная ошибка с нормальным распределением со средним 0 и дисперсией ?2.
Так как факторов более двух, графическая интерпретация модели отсутствует.
Регрессионные коэффициенты (или ?-коэффициенты) представляют независимые вклады каждой независимой переменной в предсказание зависимой переменной. Другими словами, переменная X1, например, коррелирует с переменной Y после учета влияния всех других независимых переменных.
Значения y, вычисленные с помощью регрессионной зависимости (формула 4.6) для i-го аналога, могут отличаться от значения стоимости, известной на рынке: yi = yi ~ + ?I, метод наименьших квадратов ищет коэффициенты системы уравнений (4.6) исходя из условия минимизации суммы квадратов отклонений:
Зависимой переменной в данном случае является величина рыночной стоимости 1 сотки площади объекта.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКДанный текст является ознакомительным фрагментом.