9.5. Систематическая асимметрия и эксцесс как меры риска в объяснении различий доходности акций на рынке

Статистически асимметрия и эксцесс рассматриваются как третий и четвертый моменты распределения доходности, нормализованные на кубическую и четвертую степень волатильности.

Ограничение анализа первыми двумя моментами распределения подразумевает пренебрежение значимости моментов более высокого порядка, что приемлемо только, во-первых, когда функция полезности инвесторов принимает квадратичную форму и, во-вторых, когда распределение доходностей подчиняется нормальному закону [Rubinstein, 1973]. Следует отметить, российский фондовый рынок отличается большой волатильностью и смещенностью относительно нормального распределения. Уровень ликвидности существенно различен по акциям публичных компаний. Традиционные приемы моделирования доходности на российском рынке показывают удовлетворительные результаты только в отдельные периоды развития экономики. Таким образом, по причине того, что развивающиеся рынки, и в частности российский фондовый рынок, не подчиняются нормальному закону распределения и характеризуются асимметричным распределением доходностей, для инвесторов важную роль при принятии решений начинает играть форма хвостов распределения доходностей, мерой которых могут выступать моменты более высоких порядков.

Впервые переход к систематической асимметрии (coskewness) как дополнительной мере риска предложен в работе А. Крауса и Р. Литценберга [Kraus, Litzenberger, 1976], когда стандартная двухмоментная (средняя доходность и дисперсия) модель САРМ модифицировалась путем добавления еще одной меры риска – систематической скошенности. Авторы отстаивали преимущества новой спецификации модели для объяснения связи «риск – доходность». Хотя Дж. Фрэнсис [Francis, 1975] показал, что общая (total) скошенность не значима в объяснении различий доходности акций, однако Краус и Литценберг [Kraus, Litzenberger, 1976] доказывают, что именно систематическая (co-skewness), а не общая скошенность должна вводиться в модель для объяснения уровней доходности по портфелям и активам.

Общий вид модели:

?₀ – свободный член; ?₁ – рыночная премия за систематический риск, измеряемый ? = (dR / dS)S_M; ?₂ – рыночная премия за риск, измеряемый систематической асимметрией – (-dR / dM)M_M.

Кроме того, модель Крауча и Литценберга может быть записана следующим образом [Kraus, Litzenberger, 1976]:

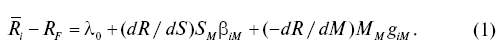
На протяжении ряда лет с 1980-х годов проводились тестирования трехфакторной САРМ, а с конца 1990-х годов появились исследования в рамках четырехфакторой САРМ с добавлением четвертого момента распределения доходностей – систематического эксцесса.

Четырехфакторная модель САРМ в уравнении представляет собой комбинацию систематической беты, систематической асимметрии и систематического эксцесса с соответствующими премиями за риск (лямбды). Если эти три фактора значимы для инвестора при объяснении доходности инвестирования, то оцененные по регрессии коэффициенты ?1, ?2, ?3 должны быть статистически значимы и отличны от нуля.

Аналитическое представление для этих мер риска имеет вид:

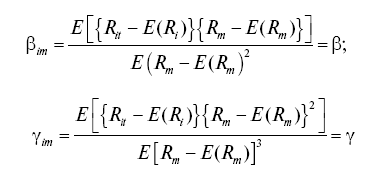
(коэффициент систематической асимметрии);

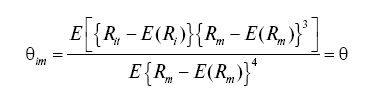
(коэффициент систематического эксцесса).

При тестировании проверяется гипотеза, что согласно свойствам функции полезности рационального инвестора рыночная премия для бета-коэффициента как показателя рыночного риска —?₁ будет положительной, знак рыночной цены систематической асимметрии – ?₂ будет противоположным знаку асимметрии распределения доходности, рыночная цена систематического эксцесса (премия) – ?₃ должна быть положительна.

Модифицированная модель САРМ прошла ряд эмпирических проверок и несмотря на неоднозначность общих выводов продемонстрировала достаточно неплохую объяснительную способность как на развитых, так и развивающихся рынках [Doan, Lin, Zurbraegg, 2010; Hung, 2007; Chiao, Hung, Srivastava, 2003]. В работе [Friend, Westerfield, 1980] представлен отрицательный результат тестирования систематической асимметрии как дополнительного объясняющего риска на отрезке 1952–1976 гг. для американского рынка акций и облигаций. Помимо акций в анализ были включены также облигации, что позволило построить авторам два варианта рисковых портфелей, первый из которых содержал как акции, так и облигации, в то время как второй строился исключительно на акциях. В качестве показателя рыночного портфеля, построенного по акциям, выступали средневзвешенный индекс и индекс, взвешенный по стоимости акций компаний. Тестирования проводились как для отдельных финансовых активов, так и для портфелей. Авторы не нашли подтверждение выводов, сделанных Краусом и Литценбергом [Kraus, Litzenberger, 1976], хотя их результаты слабо подтверждают то, что инвесторы платят премию за положительную скошенность доходностей портфелей. Авторы также отмечают факт чувствительности выводов к рыночным условиям, в частности к связи между средней рыночной доходностью и безрисковой ставкой. Основной вывод работы – степень объяснения цен отдельных финансовых активов при добавлении систематической ко-асимметрии к бета-коэффициенту находится под значительным влиянием выбора, какие рыночные индексы используются как прокси рыночных портфелей и какие процедуры оценки и тестирования проводятся. Например, эмпирические результаты выявили, что оцененная безрисковая ставка гораздо выше фактической безрисковой доходности. Как результат, авторы доказывают, что модель 3-го порядка с включением бета-коэффициента и систематической асимметрии применима для американского рынка в определенных случаях и при определенных условиях.

Кроме того, К. Лим [Lim, 1989] по данным американского рынка акций на 50-летнем временном горизонте (с января 1933 г. по декабрь 1982 г.) подтверждает, что показатель систематической асимметрии повышает объяснительную способность САРМ.

Еще одна попытка протестировать расширенную модель САРМ до 3-го порядка на американском рынке была сделана Р. Серсом и К. Веем [Sears, Wei, 1988]. Авторы использовали факт чувствительности ожидаемой премии за риск ценной бумаги i к рыночной премии за риск. Если рыночную премию за риск явным образом вставить в уравнение (1), данная модификация примет вид:

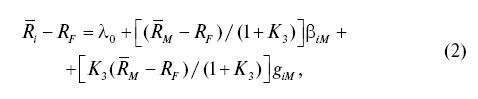
где К₃ = [(-dR /dM) / (dR/dS)](M_M/S_M) – рыночная предельная норма замещения между асимметрией и риском, нормированная на асимметрию с поправкой на риск рыночного портфеля.

К, можно преобразовать в – (dS/S_M)(dM/М_м) – как показатель перекрестной эластичности между стандартным отклонением и асимметрией. Это показывает, насколько процентов увеличится (уменьшится) стандартное отклонение доходности при увеличении положительной (отрицательной) асимметрии на 1 % при прочих равных условиях.

Исследователи гораздо реже обращали внимание на четвертый момент распределения доходности (эксцесс, kurtosis) по сравнению с моментом 3-го порядка, и на анализ влияния эксцесса на ценообразование активов. В работе [Fang, Lai, 1997] сделан вывод, что инвесторы получают компенсацию за несение риска эксцесса, так же как и за риски ковариации и систематической асимметрии (скошенности) в виде более высоких ожиданий доходности. В ряде работ [Homaifar, Graddy, 1988; Lai, 1997; Iqbal, 2007] отстаивается важность учета систематического эксцесса (соkurtosis), однако результаты эмпирических исследований, направленных на выявление значимости этой меры риска при объяснении различий доходности, неоднозначны.

Большинство исследователей развивающихся рынков капитала фокусируют свое внимание на рыночных индексах, нежели на отдельных ценных бумагах. Например, в работе [Hwang, Satchell, 1999] моменты более высоких порядков включены в модель ценообразования на развивающихся рынках капитала. В работе [Mitra, Low, 1998] сравниваются асимметрия и эксцесс при объяснении различий доходности рыночных индексов на развитых и развивающихся рынках капитала.

В работах [Ranaldo, Favre, 2005; Christie-David, Chaudhry, 2001; Chang et al., 2001; Jurczenko, Maillet, 2002; Galagedera et al., 2002] используется спецификация модели для тестирования систематической асимметрии и эксцесса, которая базируется на кубической зависимости. При этом используют данные не только акций, но и специфических портфелей. Например, в работе [Ranaldo, Favre, 2005] тестируется четырехмоментная САРМ по результатам инвестирования хедж-фондов и показано, что применение двухмоментной модели может привести к неадекватным результатам оценки компенсации за инвестиционный риск. В работе [Christie-David, Chaudhry, 2001] исследуется четырехмоментная модель на рынке фьючерсов, авторы делают вывод, что систематическая асимметрия увеличивает объяснительную способность модели на рынке фьючерсов.

В исследовании САРМ с моментами более высоких порядков на рынке Пакистана [Javid, 2009] показано, что трехмоментная САРМ относительно неплохо объясняет взаимосвязь «риск – доходность» на пакистанском фондовом рынке в исследуемом периоде времени на основе 50 компаний. Однако результаты четырехмоментной модели подчеркивают, что систематическая ковариация и систематический эксцесс не значимы в объяснении поведения цен акций, тогда как систематическая асимметрия остается значимым фактором.

Р. Доан с соавторами [Doan et al., 2010] приводит результаты тестирования более высоких моментов распределения доходностей в объяснении вариации средних доходностей акций компаний, котирующихся на американской (индекс S&P) и австралийской площадках. Сопоставление распределения доходностей выявило, что австралийские акции характеризуются более значимой отрицательной асимметрией, однако распределение менее островершинное, чем на американском рынке. Авторы приходят к выводу, что степень влияния систематической асимметрии и систематического эксцесса на ценообразование активов в целом зависит от характеристик компаний выборки и склонности инвесторов к риску. Систематическая скошенность играет более важную роль в ценообразовании австралийских акций (статистически значима на 1 %-м уровне значимости). Крометого, на американском рынке существенное воздействие на формирование цены актива оказывает систематический эксцесс, в то время как на австралийском фондовом рынке степень влияния систематического эксцесса меняется в зависимости от размера портфеля. Данный вывод подкрепляется фактом, что распределение доходностей американского рынка характеризуется более высоким выборочным эксцессом по сравнению с австралийским фондовым рынком. Авторы выдвигают гипотезу, что различия в результатах связаны с особенностями компаний, формирующих выборки: австралийские фирмы в основном меньше по размеру, чем их американские аналоги и в меньшей степени сконцентрированы в промышленном секторе. В целом авторы показали, что добавление систематической асимметрии и систематического эксцесса улучшают объяснительную способность модели (аналогично выводу М. Кахарта [Carhart, 1997]) с четырьмя факторами, включая размер компании, индикатор инвестиционных возможностей (BV/MV) и моменты более высоких порядков.

На основе конструкции, предложенной Хоганом и Варреном [Hogan, Warren, 1974], Д. Галагедераи Р. Брукс [Galagedera, Brooks, 2007] определи меру односторонней систематической скошенности (HW-gamma) следующим образом:

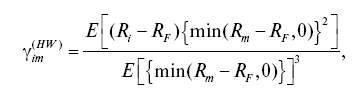
где R_i– доходность ценной бумаги i;R_m — доходность рыночного портфеля; R_F – безрисковая ставка.

Соответственно в рамках спецификации [Harlow, Rao, 1989] односторонняя систематическая скошеность (HR-gamma) примет вид:

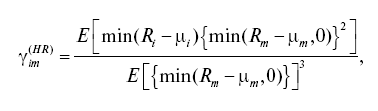
где ?_i и ?_m – средняя доходность ценной бумаги i и среднерыночная доходность соответственно.

Для спецификации модели X. Эстрады [Estrada, 2002; 2007] по аналогии с односторонним бета-коэффициентом соответствующая мера односторонней систематической скошенности (E-gamma) примет вид:

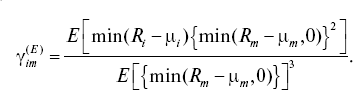
Заметим, что все избыточные доходности рыночного портфеля неположительны (min(R_m – т, 0) ? 0, где т – бенчмарк) в случае одностороннего бета-коэффициента и все принимают неотрицательное значение (min(i?_m – т, 0)]² ? 0) в случае односторонней гаммы. Более того, для одностороннего бета-коэффициента (одностороннего гамма) увеличение числителя (уменьшение) происходит, когда избыточная доходность портфеля отрицательна и уменьшение (увеличение) в случае, когда избыточная доходность портфеля положительна.

Для выборки 50 финансовых активов российского рынка рассчитанные значения гамма-коэффициента как систематической асимметрии в рамках двух спецификаций с несколькими бенчмарками и дельта как систематического эксцесса приведены в табл. 9.20 и 9.21 для двух временных отрезков. В табл. 9.22 показаны премии за риск по выделенным мерам в рамках однофакторных моделей. В табл. 9.23 и 9.24 – результаты перекрестной регрессии с включением меры Эстрада (2009), гамма и дельта.

Таблица 9.20

Меры одностороннего риска высшего порядка распределения, 2004–2007 гг. (top 10)

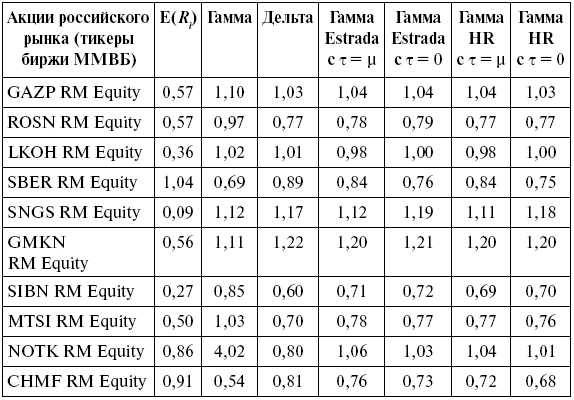
Таблица 9.21

Меры одностороннего риска высшего порядка распределения, 2008–2009 гг. (top 10)

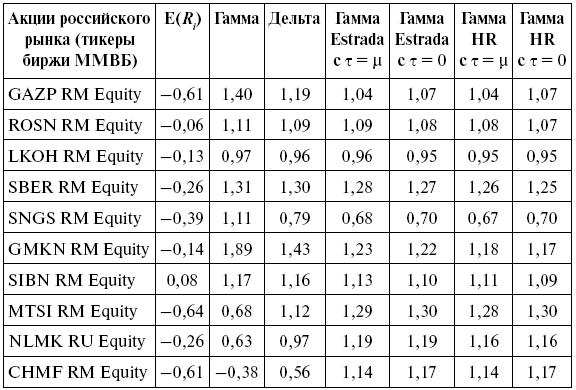
Для односторонних коэффициентов гамма и дельта лучшая объясняющая способность наблюдается в спецификациях с нулевым бенчмарком. Односторонняя систематическая асимметрия в рамках спецификации Харлоу – Рао, а также Эстрада с бенчмарком, равным нулю, показывает статистическую значимость на 5 %-м уровне. Другие меры систематического риска статистически не значимы. Значимость моделей в объяснении доходности зависит от выделенных временных периодов (финансовой стабильности и нестабильности).

Систематическая асимметрия статистически значима на 5 %-м уровне в однофакторных и двухфакторных моделях, объяснительная способность модели улучшается с введением гамма-коэффициента по сравнению с другими моделями (В² = 0,123 в однофакторных моделях и R² = 0,126 в двух факторных моделях). Лучшие результаты в объяснении различий доходности по активам наблюдаются на отрезке финансовой нестабильности (2008–2010).

Таблица 9.22

Сопоставление разных спецификаций САРМ с моментами высшего порядка (50 финансовых активов российского рынка на временных отрезках 2004–2007 и 2008–2010 гг.)

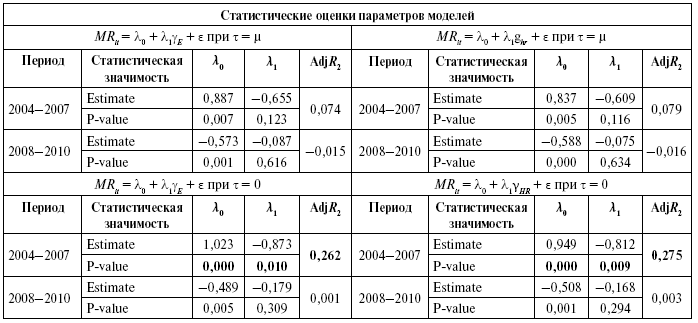
Таблица 9.23

Мера GLS (как бета-коэффициент) в расширенных моделях с асимметрией и эксцессом

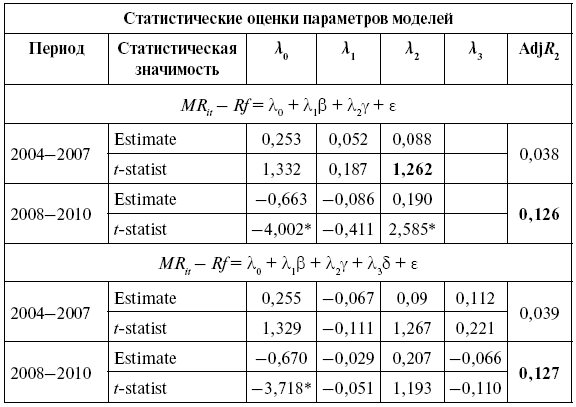
*5 %-й уровень значимости; **10 %-й уровень значимости.

Расчет проведен на основе недельных доходностей.

Таблица 9.24

Тестирование многофакторных моделей с моментами высшего порядка

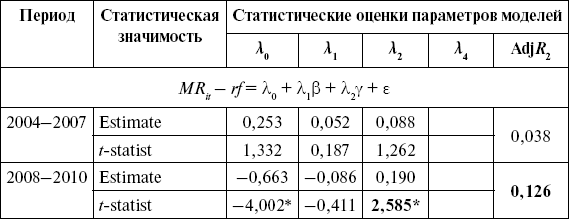
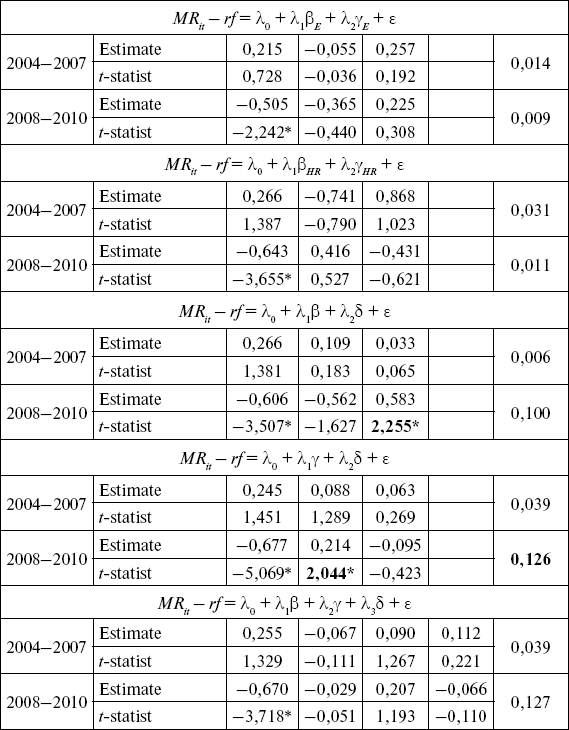
*5 %-й уровень значимости; **10 %-й уровень значимости.

Кросс-секционный анализ четырехфакторной модели САРМ показал (см. табл. 9.24), что такие параметры систематического риска, как бета, гамма и дельта, статистически не значимы, только свободный член статистически значим на 5 %-м уровне. Более того, объяснительная способность четырехмоментной модели на отрезке с 2004 по 2007 г. гораздо ниже по сравнению с качеством традиционной рыночной модели (Adji?²= 0,076). Для отрезка финансовой нестабильности качество четырехмоментной модели улучшается по сравнению со стандартной версией САРМ, но данный положительный результат не свидетельствует в пользу выбора данной спецификации модели. Данное улучшение качества модели во многом обязано высокой объясняющей способности систематической асимметрии, тем не менее все переменные в модели, включая ко-асимметрию, статистически не значимы.