9.1. Стандартное отклонение как показатель оценки риска, бета как мера риска

Критерий ранжирования и отбора финансовых активов, а также ранжирования различных портфелей на основе соотношения «средняя доходность – стандартное отношение этой доходности» (mean-variance) является основополагающим в современных финансах. Портфельная теория Г. Марковица [Markowitz, 1959] гласит, что при выборе портфеля инвесторы, используя свои кривые безразличия (indifference curves)[33], должны сопоставить все альтернативные портфели с точки зрения их ожидаемых доходностей (учитывающих прирост богатства на некотором отрезке времени) и стандартных отклонений этих приростов от среднеожидаемого значения. Учет вероятности как «плохих событий», приводящих к падению стоимости портфеля, так и «хороших», т. е. использование в качестве оценки инвестиционного риска именно дисперсии (стандартного отклонения) является неочевидным решением. Г. Марковиц в работе 1959 г. отказался от идеи учета только одностороннего отклонения доходности от заданного бенчмарка и применил трактовку риска как двустороннего отклонения от среднего значения, которая впоследствии стала классической.

Первый мотив перехода к стандартному отклонению как двусторонней оценке риска – простота вычислений. Второй мотив – фиксация на фондовом рынке нормальности кривой распределения доходности, например, по акциям. Действительно, на небольших временйых интервалах распределение доходности ценных бумаг (акций) можно признать близким к нормальному (Гауссову) распределению, которое симметрично относительно среднего значения доходности (равного медианному и модальному значению) или к логнормальному. Хотя существуют финансовые активы, которые явно не соответствуют таким предположениям нормальности или логнормальности распределения доходности. Графически различия между нормальным и логнормальным распределением богатства S показаны на рис. 9.1.

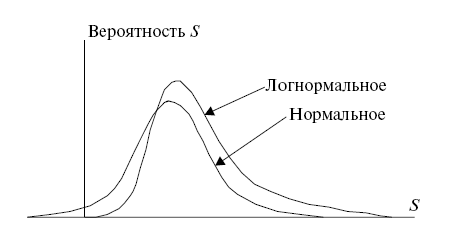
Рис 9.1. Традиционно используемые предположения о вероятностном распределении доходностей ценных бумаг

Например, опционы или ценные бумаги с включенными опционами (конвертируемые, отзывные облигации, привилегированные акции) заведомо не характеризуются нормальным распределением (см. рис. 9.1). Отбор портфелей таких активов должен учитывать специфику вероятностного распределения выгод по ним. Более того, можно утверждать, что ни одна мера риска не может претендовать на точность результатов в оценке эффективности инвестирования, при объяснении различий доходностей в любых обстоятельствах. Анализ рыночной среды и особенностей поведения доходности рассматриваемых активов должен позволить выработать адекватные меры для сопоставления и ранжирования этих активов по инвестиционной привлекательности.

Базируясь на положениях портфельной теории Г. Марковица и критерии сопоставления портфелей «средняя доходность – стандартное отклонение»[34] У. Шарп (1964), Дж. Линтнер (1965) и Ж. Мосин (1966) разработали равновесную модель ценообразования финансовых активов (портфелей акций), которая объясняла взаимосвязь ожидаемой и требуемой доходностей по портфелю и инвестиционным риском этого портфеля (Capital Assets Pricing Model – САРМ). Одновременно были предложены портфельные оценки эффективности инвестирования (performance measures), которые базируются на критерии «средняя – стандартное отклонение»: индекс Трейнора (1965), коэффициент Шарпа (1966) и альфа-коэффициент Дженсена (1968).

Коэффициент Шарпа (Sharp ratio – SR, или reward to variability ratio – RVarR) показывает результат инвестирования в виде избыточной доходности, приходящийся на единицу риска, когда мерой риска выступает стандартное отклонение. Коэффициент Шарпа показывает дополнительную доходность (премию), получаемую инвестором относительно безрисковой ставки на единицу общего инвестиционного риска.

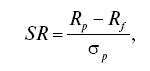
где R_p – расчетная доходность актива или портфеля (например, за месяц, год); ?_p – стандартное отклонение доходности этого портфеля; R_? – безрисковая ставка доходности на рынке, как доходность, принимаемая для безрискового актива.

Индекс Трейнора (Treinor Index или Reward to Volatility Ratio – RYolR) в отличие от коэффициента Шарпа в качестве показателя риска рассматривает не общий риск, а только его систематическую часть, выраженную через бета-коэффициент (как коэффициент эластичности доходности портфеля к доходности хорошо диверсифицированного портфеля).

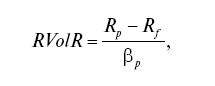
где бета-коэффициент портфеля – оценка систематического риска этого портфеля, как отношение коэффициента ковариации доходностей портфеля (Р) и рынка (М) к дисперсии доходности рынка (фондового индекса):

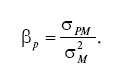
Альфа-коэффициент Дженсена (Йенсена) рассматривается как мера несистематического риска портфеля, это результат, который может быть расценен как вклад в доходность управляющего портфелем. Альфа-коэффициент (а) рассчитывается по рыночной модели, увязывающей премию за инвестирование в портфель (MRP = R_p – R_?) с ожидаемой премией за систематический риск, которая пропорциональна бета-коэффициенту портфеля. Альфа-коэффициент показывает переоценку или недооценку рынком систематического риска портфеля (или отдельного актива). Рыночная модель: R_p – R_? = ?_p?MRP+?_p, соответственно

?_p=R_p-[R_? + ?·MRP].

Все три портфельные меры риска подразумевают, что доходность рассматриваемых портфелей нормально распределена и инвестор сопоставляет активы по риску и выгодам на основе критерия «средняя – стандартное отклонение» (mean variance analysis framework). На этом же предположении строится и модель САРМ.

Ключевая идея САРМ заключается в наличии линейной связи между доходностью актива (R) и мерой его систематического риска, определяемой бета-коэффициентом: E(R_i) = R_?+ ? [E(R_M) – R_?].

Заметим, что в практике инвестиционного анализа приемлемы два подхода к расчету доходности. Процентная (дискретная) доходность с момента времени t до момента i: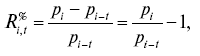

где р_i – цена актива в i-й период времени.

Логарифмическая (непрерывная) доходность с момента времени t до момента i: 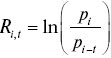. При работе с финансовыми активами довольно часто используют логарифмическую доходность. Преимущество ее использования двояко: во-первых, она может быть экономически более содержательной, чем процентная доходность. Если логарифмическая доходность распределена нормально, распределение не приведет к отрицательной цене (в «левом хвосте» распределения логарифмы отношения цен стремятся к «минус бесконечности» при текущей цене, стремящейся к нулю. Напротив, в «левом хвосте» нормально распределенной доходности величина стремится к «минус бесконечности» при отрицательной величине текущей цены, что экономически бессмысленно). Второе преимущество логарифмических доходностей состоит в том, что они хорошо агрегируются во времени. Логарифмическая доходность от момента времени t до момента времени Т эквивалентна сумме логарифмических доходностей на интервалах от t до ? и от ? до Т, где t? ? ?T:

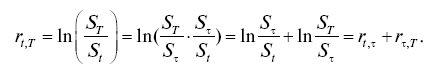
Эта временна?я аддитивность логарифмических доходностей говорит о том, что если однопериодные доходности независимы, волатильность доходностей масштабируется на квадратный корень из времени (?T?). Однако процентные (дискретные) доходности имеют преимущества для случаев, когда ставится задача агрегировать активы в портфель. Например,

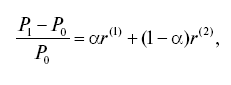
где ? – доля портфеля, вложенная в акцию; r⁽¹⁾ – доходность акции; r⁽²⁾ – доходность облигации; Р_i – стоимость портфеля в i-й момент времени (Р₀ – стоимость портфеля в начальный момент; Р₁ – стоимость портфеля на конец периода).

В то же время логарифмическая доходность портфеля не является средневзвешенным логарифмических доходностей активов, входящих в портфель.

Насколько модель САРМ позволяет объяснить различия в доходностях отдельных акций или портфелей, зависит от соответствия достаточно жестких предпосылок модели рыночным реалиям. На протяжении многих лет от первых публикации по САРМ проводится тестирование модели на предмет объяснительной силы в наблюдаемых различиях доходности по активам рынка (cross-section return variations)[35], а также возможности предсказать будущую доходность (test of predictability) по той или иной ценной бумаге (портфелю) на основе моделирования риска[36]. Хотя тесты на предмет объяснительной способности САРМ однозначно не дают положительных ответов, однако на практике модель получила огромное признание и распространение.

В расчетах аналитиков инвестиционных компаний и менеджеров нефинансовых корпораций модель САРМ и конструкция дисконтированных денежных потоков (discounting cash flow, DCF) занимают лидирующие позиции. Ведущие информационно-аналитические агентства (Bloomberg, YalueLine, DataStream, Merrill Lynch, Thomson Reuters) включают информацию о параметрах САРМ (регрессионный бета-коэффициент, скорректированный бета-коэффициент, безрисковая ставка) для компаний разных рынков. Ежегодные опросные исследования более 11 тыс. финансовых директоров США, проводимые периодически Duke University и CFO Magazine, показали, что и в докризисные годы, и в 2008–2009 гг. порядка 75 % респондентов при принятии инвестиционно-финансовых решений ориентировались на САРМ [Graham, Harve, 2009]. Анализ публичных аналитических отчетов 38 инвестиционных компаний, работающих на российском рынке капитала [Teplova, 2010], показал, что в рамках конструкции дисконтированных выгод большинство аналитиков ориентируются на конструкцию САРМ с введением странового риска через поправку на относительную волатильность российского рынка по сравнению с глобальным. Значение бета-коэффициента в большинстве отчетов вводится на отраслевом уровне по глобальным компаниям или через экспертные оценки с учетом низкой ликвидности рассматриваемых акций.