13.5.1. Уравнения для розничной торговли

13.5.1. Уравнения для розничной торговли

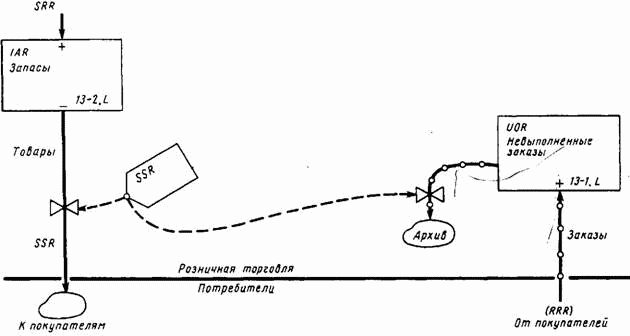
Рис. 13-2. Исходная диаграмма потоков в розничной торговле.

Мы начнем с двух простых уравнений: одно описывает уровень невыполненных заказов, другое — запасы товаров. На рис. 13-2 показаны эти две переменные на первой стадии построения диаграммы потоков. Здесь IAR — запасы товаров, а сплошные линии изображают входящие и исходящие потоки материалов; UOR — уровень невыполненных заказов; соответствующие потоки изображены линиями с кружками, идущими к прямоугольнику и от него. Величина UOR может быть определена с помощью обычного уравнения уровня, который зависит от темпов одного входящего и одного исходящего потоков[67].

,

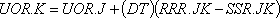13-1, L

где

UOR — заказы, не выполненные розницей (в единицах товара);

RRR — требования (заказы), получаемые розницей (единицы в неделю);

SSR — розничная отгрузка (единицы в неделю);

DT — интервал времени между решениями уравнений (недели).

В указанном справа порядковом номере уравнения цифра 13 означает номер, главы цифра 1 — номер уравнения внутри главы, а индекс L указывает, что это уравнение описывает уровень. Уравнение определяет количество невыполненных заказов в настоящий момент времени К, исходя из количества невыполненных заказов, определенного в последний раз для момента времени Y, и из темпов входящего и исходящего потоков в интервале времени JK между вычислениями. Темпы входящих и исходящих потоков в течение интервала JK принимаются постоянными (для того, чтобы это допущение было приемлемым, интервал времени должен быть достаточно коротким). Произведение продолжительности интервала времени DT на темп входящего потока RRR. JK определяет число новых заказов, полученных за интервал JK. Точно так же произведение (DT)(SSR.JK) определяет количество заказов, выполненных в течение этого же интервала. Обе части уравнения имеют одинаковую размерность:

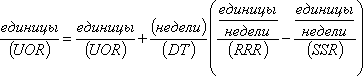
Интервал времени между решениями DT должен быть коротким по сравнению с величиной отображаемых в модели запаздываний[68]. В нашем примере интервал решений должен быть небольшой частью недели. Темпы потока при такой формулировке уравнения измеряются в общепринятых единицах (например, недельный темп), и уравнение остается справедливым независимо от длины интервала DT. Это оставляет достаточную свободу для выбора интервала времени DT между решениями в соответствии с критериями, которые будут рассмотрены ниже.

На рис. 13-2 для полноты учета всех видов потока показан архив выполненных заказов, исключаемых из действующей системы.

Второе уравнение, описывающее уровень запасов в розничной торговле, по существу аналогично первому:

,

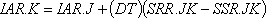13-2, L

где

IAR — фактический запас в рознице (единицы);

SRR — поставки, получаемые розницей (единицы в неделю);

SSR — розничная отгрузка (единицы в неделю).

Приведенные уравнения, описывающие уровни, просты и неопровержимы. Они представляют собой основу описания системы. Эти уравнения отражают тот факт, что действительный остаток определяется путем последовательного прибавления или вычитания количеств, определяемых темпами входящего и исходящего потоков.

Уравнения темпов, напротив, не являются столь очевидными и простыми. Именно в уравнениях темпов отображается механизм решений, свойственный системе. Уравнения темпов отражают наше понимание факторов, определяющих действия. Решения, которые регулируют темпы и лежат в основе уравнений темпов, должны быть сформулированы таким образом, чтобы уравнения оставались справедливыми и достаточно точными при любых, даже самых больших изменениях значений переменных, которые могут иметь место в системе. Уравнения темпов часто включают нелинейные функциональные зависимости, описывающие реальное поведение системы в различных обстоятельствах.

Вопреки обычному представлению требование, чтобы уравнения темпов были верными при экстремальных значениях входящих в них переменных, скорее облегчает, чем затрудняет, построение полезной модели. Очень часто при определении экстремальных условий, которые могут иметь место на практике, мы можем хорошо обрисовать границы, в которых должна действовать система. Когда эти границы установлены, влияние промежуточных функциональных взаимосвязей между причиной и следствием часто становится пренебрежимо малым. Все зависимости, удовлетворяющие известным ограничительным условиям, могут часто давать почти одни и те же результаты. Уравнение темпа может быть построено на основе рассмотрения различных обстоятельств, оказывающих влияние на темп потока. Для того чтобы это проиллюстрировать, начнем с определения темпа отгрузки товаров из розницы покупателям SSR.

Здесь под темпом отгрузки товаров покупателям понимается объективно обусловленный темп. Это значит, что он определяется состоянием системы, а не чьим-либо произвольным административным решением. В принципе можно представить себе решение вообще не посылать имеющиеся товары; однако встречается оно редко, и мы будем им пренебрегать. С математической точки зрения нет никакой разницы между уравнениями явных и неявных решений. Однако определение вида решения обычно помогает внести ясность в наши мысли при построении уравнения.

Темп отгрузки товаров покупателям должен зависеть от величины задолженности по невыполненным заказам, по которым товары подготовлены к отправке. В предельном случае, когда нет заказов, не будет и поставки. Точно так же возможность поставить товары должна зависеть от наличия запасов, из которых может производиться поставка. Темп поставок не зависит от каких-либо других темпов, имеющих место в системе в тот же момент времени. Возможность поставки в данный момент зависит от наличия невыполненных заказов, но не зависит от существующего в данный момент времени темпа поступления новых заказов, так как товары по ним в этот момент еще не могут быть предметом поставки. Только уровень имеющихся товаров, а не темп их поступления в розничную торговлю SRR и не темп размещения заказов в оптовом звене влияет на возможность поставок в настоящий момент, хотя уровни, определяющие возможность поставок в данный момент, достигли своей теперешней величины под влиянием определенных темпов этих потоков в прошлом. Имеющие место в данный момент темпы ряда потоков воздействуют на будущую, а не на настоящую возможность поставок. Если читателю кажется, что другие темпы потоков, имеющие место в настоящее время, влияют на темп поставок в данный момент времени, значит, он не смог увидеть разницу между мгновенными и средними темпами или не разобрался в достаточной мере в вопросе о том, что понимается под настоящим моментом времени.

Есть, очевидно, много приемлемых способов построения уравнения темпа поставки товаров. Мы здесь будем считать, что темп выполнения заказов определяется объемом невыполненных заказов и запаздыванием выполнения заказов, которое является переменной величиной. В свою очередь запаздывание выполнения заказов мы будем рассматривать как функцию имеющихся запасов.

При таком способе определения темпа поставок мы можем получить следующее простое уравнение:

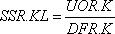
SSR — розничная отгрузка (единицы в неделю);

UOR — заказы, не выполненные розницей (единицы);

DFR — запаздывание (переменное) выполнения заказов розницей (недели).

Это уравнение имеет форму показательного запаздывания первого порядка[69] только без учета того обстоятельства, что запаздывание может быть переменной величиной. Из приведенного уравнения следует, что недельный темп поставок в данное время составляет определенную часть всех невыполненных заказов, равную 1/DFR.K. В известном смысле это уравнение определяет, что именно подразумевается под запаздыванием DFR. Мы можем проверить, насколько удовлетворительной может быть эта зависимость в различных несложных обстоятельствах.

Прежде всего представим себе стабильные условия, при которых имеет место постоянный поток заказов RRR и постоянный, стабильный темп розничной отгрузки SSR. Из уравнения следует, что при постоянном темпе отгрузки чем больше запаздывание DFR, тем больше скапливается невыполненных заказов UOR. Это соответствует действительности, поскольку в стабильных условиях объем заказов в стадии исполнения должен быть пропорционален и темпу продаж SSR, и среднему запаздыванию в выполнении имеющихся заказов.

Рассмотрим некоторые частные случаи использования приведенного выше уравнения. Если бы в системе, находившейся в стабильных условиях, неожиданно возрос темп поступления заказов RRR, то реакция темпа отгрузки SSR имела бы характер, показанный на рис. 13-3. Такая реакция соответствует показательному запаздыванию первого порядка. Показанная на рис. 13-3 зависимость между заказами и поставками представляется правдоподобной. Действительно, если товары продаются не с прилавка (как, например, холодильники), то темп действительной отгрузки будет повышаться постепенно вслед за повышением темпа продажи. Заштрихованная площадь между кривой продаж RRR и кривой поставок SSR представляет собой объем дополнительных заказов, находящихся в стадии выполнения, которые присоединяются к невыполненным заказам UOR, как это уже рассматривалось применительно к стабильным условиям.

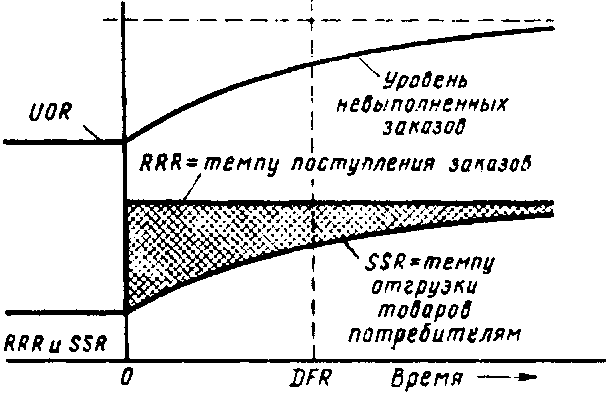
Рис. 13-3. Реакция темпа отгрузки товаров покупателям SSR и уровня невыполненных заказов UOR на скачкообразное изменение в темпе поступления заказов RRR.

Можно проанализировать другой частный случай. Предположим, что входящих заказов RRR не было вовсе (см. рис. 13-4). Затем появляется непредвиденная партия заказов, после чего темп заказов снова становится равным нулю; здесь мы наблюдаем так называемую «импульсную» реакцию, которая соответствует поведению запаздывания первого порядка. Мы видим, что объем невыполненных заказов резко возрос до величины, соответствующей полученной партии заказов; темп отгрузки товаров возрастает до максимума и затем снижается по мере того, как снижается задолженность по невыполненным заказам. Это можно объяснить тем, что имеются изделия, заказы на которые легко выполнимы, и по этим заказам тотчас же производятся необходимые операции. Однако мы можем получить более правильные результаты, если введем первоначальное запаздывание отгрузки; более равномерное увеличение темпа отгрузки в рассматриваемом с целью исследования модели случае представляется более реальным. Если это так, то процесс выполнения заказов может быть разделен на две или большее число стадий. Одно уравнение, как приведенное выше, могло бы отвечать запаздываниям в условиях отсутствия товарных запасов. В предшествующем случае запаздывание третьего порядка в потоке входящих заказов RRR могло бы отражать запаздывание в системе, связанное с оформлением заказа. Анализируя подобные альтернативы, можно определить их воздействие на поведение системы. Основываясь на накопленном ранее опыте, допустим, что такой детальный анализ для достижения поставленных здесь целей не требуется.

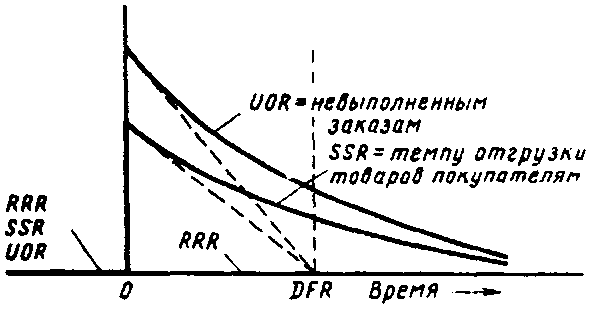
Рис. 13-4. Реакция темпа отгрузки товаров покупателям SSR и уровня невыполненных заказов UOR на импульсный ввод заказов RRR.

По приведенному выше уравнению нельзя судить с достаточной уверенностью о том, что темп отгрузки SSR в течение начального интервала времени KL будет не больше, чем это позволяют оставшиеся запасы товаров. Как будет отмечено позже при рассмотрении запаздывания DFR.K, величина этого запаздывания будет возрастать по мере сокращения запасов, в результате чего темп отгрузки будет иметь тенденцию к понижению. Все же для того, чтобы полностью исключить возможность появления отрицательных запасов, в последующих уравнениях будут специально введены две вспомогательные переменные.

В последующих трех уравнениях показан простейший прием, применяемый при построении модели. Эти уравнения были введены на ранней стадии построения данной модели и оставлены здесь как основа для обсуждения вопросов, затрагиваемых ниже (см. сноску на этой странице). Предыдущее уравнение мы перепишем, используя вместо темпа поставок SSR вспомогательную переменную STR.

,

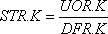13-3, A

где

STR — проверяемый темп розничной отгрузки (единицы в неделю);

UOR — заказы, не выполненные розничным звеном (единицы);

DFR — запаздывание выполнения заказов розничным звеном (недели).

Это вспомогательное уравнение, a STR — вспомогательная переменная; она вычисляется сразу после определения вспомогательной переменной DFR. Как уже отмечалось в разделе 6.4, вычисление вспомогательных переменных часто требует определенной последовательности.

Прежде чем признать, что предполагаемый темп поставки STR является истинным значением темпа поставки SSR, сопоставим значение STR с предельным темпом отгрузки, при котором за время между решениями уравнений используется весь имеющийся объем товарных запасов. Этот темп определяется следующим уравнением:

,

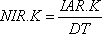13-4, A

где

NIR — предельный темп розничной отгрузки

(единицы в неделю);

IAR — фактический запас в розничном звене (единицы);

DT — интервал времени между решениями уравнений (недели).

Мы теперь готовы к тому, чтобы написать наше уравнение для темпа поставок:

,

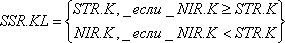13-5, R

где

SSR — розничная отгрузка (единицы в неделю);

NIR — предельный темп розничной отгрузки (единицы в неделю);

STR — проверяемый темп розничной отгрузки (единицы в неделю).

Уравнение 13-5 определяет темп розничной отгрузки, который будет иметь место в течение предстоящего интервала времени KL[70]. В нем утверждается, что если предельный темп NIR.K, определяемый из уравнения 13-4, больше или равен желаемому темпу отгрузки STR.K, определяемому по уравнению 13-3, то следует принять темп STR.K. Если NIR.K меньше, чем STR.K, то за темп поставки принимается NIR. В обычных обстоятельствах, когда запасы не снижаются до нуля, темп поставок определяется уравнением 13-3.

Взаимосвязь уравнений 13-3, 13-4 и 13-5 представлена на диаграмме потоков (рис. 13-5).

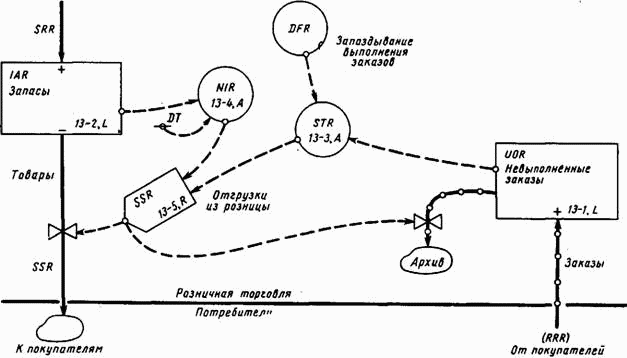
Рис. 13-5. Отражение выполнения заказов в диаграмме потоков розничной торговли.

Прежде чем перейти к составлению уравнения взаимосвязи между запасами и переменным запаздыванием DFR, используемым при вычислении темпа отгрузки товаров, необходимо более подробно остановиться на природе рассматриваемых запасов. Если мы рассматриваем один вид товара на одном складе, то ясно, что заказы могут выполняться до тех пор, пока не истощатся все имеющиеся запасы. Это показано на рис. 13-6, где все входящие заказы могут выполняться, пока на складе есть запасы. Возможность выполнения заказов сразу падает до нуля, как только истощаются запасы товаров.

Рис. 13-6. Выполнение заказов на один вид товара с одного склада.

Совсем другое положение складывается, когда один вид товара имеется в наличии на нескольких складах или множество разных товаров находится на одном складе и, уж конечно, если речь идет о множестве различных товаров на многих складах. В любом из этих случаев мы можем ожидать, что запасы одних товаров будут исчерпаны раньше других на некоторых складах и что наша суммарная возможность выполнять заказы будет постепенно снижаться по мере того, как снизится общий объем запасов всех видов товаров. Это показано на рис. 13-7. Мы будем рассматривать в нашем примере именно этот случай, поскольку имеется в виду производство различных видов товаров и их розничная продажа по всей стране.

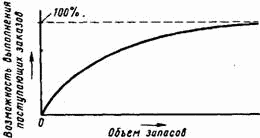
Рис. 13-7. Выполнение заказов на различные товары со многих складов.

Величина запаздывания, определения по среднему числу выполненных заказов, будет обратно пропорциональна возможности выполнения заказов. По мере того как все меньшее и меньшее число заказов может быть выполнено за счет запасов, все больше и больше невыполненных заказов будет ждать выполнения за счет поступающих товаров. На рис. 13-8 показан общий вид взаимосвязи, которая должна существовать между запаздыванием в выполнении заказа и уровнем запасов. При достаточно большом запасе товаров среднее запаздывание выполнения заказов будет приближаться к минимально возможному запаздыванию, определяемому затратами времени на оформление заказа и отгрузку товара. По мере уменьшения общего запаса, состоящего из различных товаров, все больше и больше заказов на все большем и большем числе складов будет сталкиваться с отсутствием необходимых запасов. Пока эти заказы ждут поступления соответствующих товаров, они способствуют увеличению среднего запаздывания, определяемого для всех заказов в целом. Когда запасы приближаются к нулю, запаздывание будет резко увеличиваться, устремляясь к бесконечности. Это означает, что когда нет запасов, то нет и возможности осуществлять поставки.

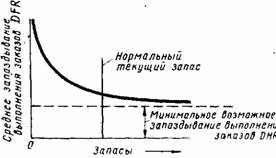
Рис. 13-8. Зависимость запаздывания от величины запаса.

Теперь можно обсудить методику вычисления переменного запаздывания DFR. Обращаясь к рис. 13-8, мы видим, что кривая, отображающая соотношение между запаздыванием и запасом, должна иметь следующую форму: она должна начинаться с какого-то минимального значения при высоком уровне запаса и затем подыматься все круче и круче по мере уменьшения запаса. Приводимое ниже уравнение удовлетворительно описывает форму такой кривой:

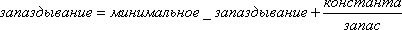
Для очень больших запасов второй член правой части уравнения близок к нулю, так что запаздывание равно минимально возможному; когда запасы приближаются к нулю, этот член выражения стремится к бесконечности, резко повышая величину запаздывания.

Такая формулировка имеет серьезный недостаток. Она основана на абсолютном уровне запасов, не вытекающем из среднего уровня деловой активности, который должен служить указанием на то, какого объема запасов «хватает». В качестве меры запаса здесь лучше, вероятно, использовать не фактический запас, а его отношение к такому запасу, который был бы «достаточным» или «соответствующим». Мы введем поэтому понятие «желательного запаса», с которым будем сравнивать фактический запас. Кривая, изображенная на рис. 13-8, в этом случае преобразуется в кривую, показанную на рис. 13-9[71].

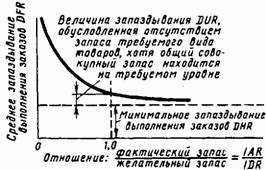
Рис. 13-9. Зависимость запаздывания от отношения фактического и желательного запасов.

Подставив в приведенное уравнение отношение запасов IAR/IDR, после простого преобразования получим следующее уравнение, которое отражает отношение между запасом и запаздыванием отгрузки товаров, о котором уже говорилось:

,

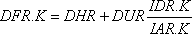13-6, A

где

DFR — запаздывание выполнения заказов розничным звеном (недели);

DHR — минимальное запаздывание выполнения заказа розничным звеном (недели);

DUR — среднее запаздывание выполнения заказов розничным звеном, связанное с отсутствием на складе некоторых товаров, при общем «нормальном» объеме запасов (недели);

IDR — желательный запас в розничном звене (единицы);

IAR — фактический запас в розничном звене (единицы).

В уравнении 13-6 общая величина запаздывания выполнения заказа равна сумме минимального запаздывания и произведения константы на отношение между желательным и фактическим запасами. После составления этого уравнения диаграмма потоков становится такой, как это показано на рис. 13–10. Теперь, когда установлены константы DHR и DUR, нам известны все величины, входящие в уравнение 13-6, за исключением величины желательного запаса IDR.

Понятие «желательный запас», который можно рассматривать как «идеальный» или «планируемый» уровень запаса, является очень важным. Оно будет здесь использовано в двух случаях. Как указывалось выше, этот потребный запас служит эталоном, с которым сравнивается фактический запас с целью установления возможности выполнения заказов. «Желательный уровень запасов» будет также одним из факторов, влияющих на формирование решения о размещении заказов на поставку товаров для создания новых запасов. Использование понятия «идеальный запас» в расчете восполнения запасов делает это понятие важным при рассмотрении динамического поведения системы. Взаимосвязь между изменениями объема запасов и среднего уровня продажи товаров является одним из нескольких наиболее важных источников усиления колебаний производственной деятельности. Независимо от стабильности системы общепринятая практика заключается в создании или уменьшении запасов в соответствии с увеличением или снижением уровня продажи товаров. Именно это дает возможность измерять запасы определенным числом недель, в течение которых можно осуществлять продажу за счет запасов; такой способ измерения запасов применяется во многих складских операциях. Понятие «годовой темп оборота запасов» также связано с представлением о пропорциональности между запасами и уровнем продаж[72].

Анализ данных о взаимосвязи между продажей товаров и общими запасами в целом по стране указывает на тенденцию выравнивания амплитуд их колебаний. Поскольку во многих случаях принимают прямую пропорциональную связь между желательным запасом и средней продажей товаров, то мы также начнем с введения такой связи:

,

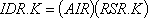13-7, А

где

IDR — желательный запас в розничном звене (единицы);

AIR — коэффициент пропорциональности (недели);

RSR — усредненные требования к розничной торговле, то есть средний темп продаж (единицы в неделю).

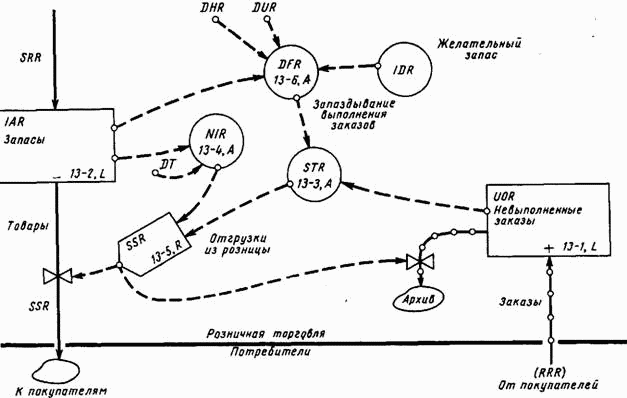
Рис. 13–10. Отражение запаздывания поставок в диаграмме потоков розничной торговли.

Константа AIR представляет собой число недель, в течение которых средний темп продажи может быть обеспечен за счет желательного запаса. Разделив это число на 52 недели, можно получить темп годового оборота запасов. Здесь снова следует напомнить читателю, что эти уравнения «правильны» только в том смысле, что они отражают те взаимосвязи, которые будут иметь место в создаваемой модели. Они не обязательно уместны и верны во всех ситуациях, складывающихся в реальной системе. Изменения, которые будут внесены в уравнение 13-7 позднее, могут быть эффективно использованы для того, чтобы найти пути повышения стабильности производственно-сбытовой системы и уменьшения ее чувствительности к внешним воздействиям, вызывающим нарушения этой стабильности.

Взаимосвязи, описываемые уравнением 13-7, включены в диаграмму на рис. 13–11. Кроме того, на ней показан поток информации, необходимой для определения среднего темпа продаж RSR. В связи с тем, что текущий темп продаж RRR будет колебаться от одного дня к другому и не будет соответствовать усредненному потоку информации, необходимо усреднить фактические данные о продаже товаров, чтобы получить цифры, на которых можно было бы основывать планы в отношении объема запасов и заказов. Чем больше «помех» в данных о продаже, тем большим должно быть время усреднения. Чем больше время усреднения, тем больше момент времени, в который определяется средний темп продажи товаров, будет отставать от реальных событий. Фактические данные требуют усреднения, усреднение порождает запаздывание, а запаздывание влияет на поведение и стабильность системы. Усреднение должно быть одной из характеристик системы, даже если мы изучаем реакцию системы на свободные от помех сигналы, хотя свободные от помех компоненты информации искажаются тем самым усреднением, которое призвано помочь нам устранить помехи. Можно использовать различные методы усреднения. Здесь мы используем «показательное усреднение первого порядка», которое дает нам уравнение следующего вида:

,

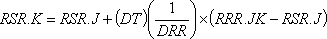13-8, L

где

RSR — усредненные требования к розничному звену (единицы в неделю);

RRR — требования, получаемые розничным звеном; текущий темп продаж (единицы в неделю);

DRR — запаздывание усреднения требований к розничному звену, постоянная времени усреднения (недели).

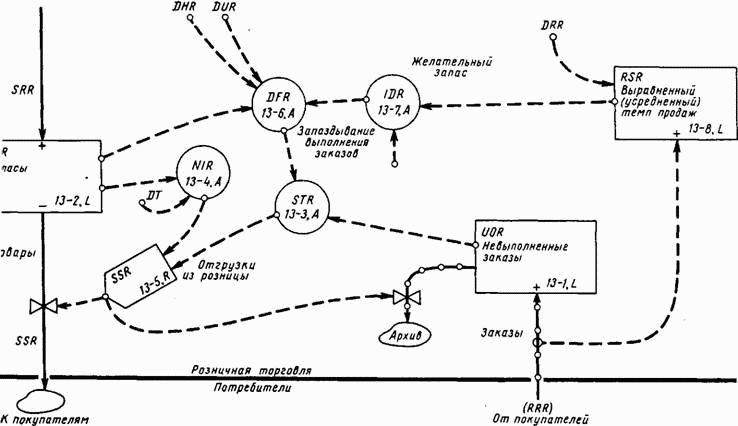
Рис. 13–11. Отражение желательного запаса и усредненного темпа продаж в диаграмме потоков розничной торговли.

Уравнение 13-8 показывает, что вновь рассчитанный средний уровень[73] продаж RSR в настоящий момент времени К равен предшествующему значению этого уровня, скорректированному на некоторую долю разности между темпом продаж в течение последнего интервала времени RRR.JK и рассчитанным ранее средним темпом продаж RSR.J. Константа DRR дает ту долю разности, на которую необходимо каждую неделю корректировать темп продаж товаров; обратная этой константе величина умножается на значение интервала времени DT, чтобы определить поправку в среднем темпе продаж за интервал времени между вычислениями. Усреднение, в основе которого лежит зависимость, описываемая показательной функцией, дает наиболее весомый результат в том случае, когда оно охватывает данные, полученные в самое последнее время.

В предыдущих уравнениях и на рис. 13–11 показаны поступающий от покупателей поток заказов розничной торговле и факторы, определяющие выполнение этих заказов. Следующий шаг состоит в разработке критерия для принятия решения о выдаче заказа оптовой базе. Это будет уравнение темпа выдачи исходящих заказов. Принимаемое в соответствии с этим уравнением решение будет явным по форме, поскольку предприниматели в розничной торговле имеют возможность заказывать любое желаемое количество товара. Будет ли иметь место поставка товаров — это определяется неявными решениями в звене оптовой торговли, которые зависят от возможности поставки этим звеном заказанных товаров

В связи с принятием решений о заказах, направленных на пополнение запасов, возникает одна проблема методологического характера. Здесь мы очень часто будем иметь дело с решениями, которые формируются постепенно. Они требуют сбора данных, предположений, рекомендаций и проверки. После этого принимается решение, которое впоследствии реализуется. При размещении заказов на пополнение запасов используются надежные источники информации, принимаются различные вспомогательные решения, обосновываются предположения о спросе и учитываются запаздывания, связанные с оформлением документов при выдаче заказов. Подробности отдельных этапов принятия решения и отдельные запаздывания в этом процессе не представляют для нас интереса с точки зрения изучения основных обобщенных характеристик производственно-сбытовой системы. При нашей формулировке уравнения запаздывания рассматриваются отдельно от решений. Нам нужно решить, как сгруппировать запаздывания и решения и установить соотношения между ними. Рис. 13–12 иллюстрирует два из многих возможных вариантов комбинаций запаздываний и решения.

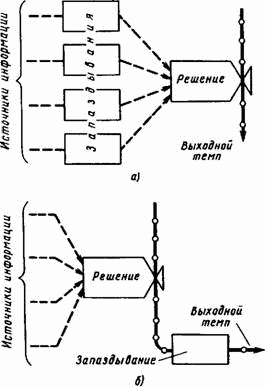
Рис. 13–12. Запаздывания получения информации и принятия решения.

На рис. 13–12 а информация от каждого из ее источников поступает со своим запаздыванием к месту принятия решения, где она объединяется для регулирования темпа на выходе. На рис. 13–12 б показан альтернативный вариант, где решение принимается на основе информации, получаемой без задержек, а затем на выходе из пункта принятия решения имеется запаздывание, которое отражает как задержки в получении информации, так и задержки при принятии решения. Для большей достоверности иногда целесообразно включить соответствующие запаздывания перед принятием решения и после него. Показанный на рис. 13–12 б метод проще, так как в этом случае для запаздывания требуется составить лишь одну систему уравнений, а не несколько. Поскольку с точки зрения поставленных здесь целей точность в представлении системы не является существенным преимуществом того или иного метода, мы выберем более простой подход, соответствующий изображенной на рис. 13–12 б схеме. Это значит, что мы будем строить уравнение для определения «предстоящего» решения о выборе темпа закупок, вводя в него запаздывание в потоке заказов, которое по величине будет эквивалентно общему запаздыванию обработки исходных данных, принятия решения о закупке товаров и оформления заказа на пополнение запаса в закупочной конторе.

Первая задача состоит в том, чтобы выявить основные источники информации, которые должны оказывать влияние на темп закупок. Мы уже решили не включать в модель прогнозы, а также и ряд других мало существенных факторов. Первый из наиболее важных, подлежащих учету факторов — это возобновление запасов товаров взамен проданных. Кроме того, необходимо предусмотреть размещение заказов для компенсации разницы между фактическим и желательным запасами. Необходимо также установить так или иначе неизбежное увеличение объема заказов и товаров, нужных для заполнения каналов системы.

Если установлено определенное время передачи заказов и товаров по каналам между розничной и оптовой торговлей, то необходимо, чтобы общее количество заказов и товаров в каналах было пропорционально уровню деловой активности. Если не вводить заказы с этой целью в каналы системы, то возникнет недостаток запасов. Эти факторы выражены в следующем уравнении:

,

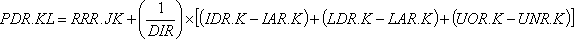13-9, R

где

PDR — темп закупок розницей, устанавливаемый в результате решения (единицы в неделю);

RRR—требования, получаемые розничным

звеном (единицы в неделю);

DIR — запаздывание регулирования запасов (и заполнения каналов) в розничном звене (недели);

IDR — желательный запас в розничном звене (единицы);

IAR — фактический запас в розничном звене (единицы);

LDR — желательный уровень передаваемых по каналам заказов, определяемый потребностями розничной торговли (единицы);

LAR—фактический уровень выданных розничным звеном заказов, находящихся в каналах (единицы);

UOR — заказы, не выполненные розничным звеном (единицы);

UNR — нормальное для розничного звена число невыполненных заказов (единицы).

Диаграмма потоков, построенная с учетом уравнения 13-9, показана на рис. 13–13. Ниже будут рассмотрены все члены этого уравнения, определяющего темп выдачи заказов на товары в течение предстоящего интервала времени KL.

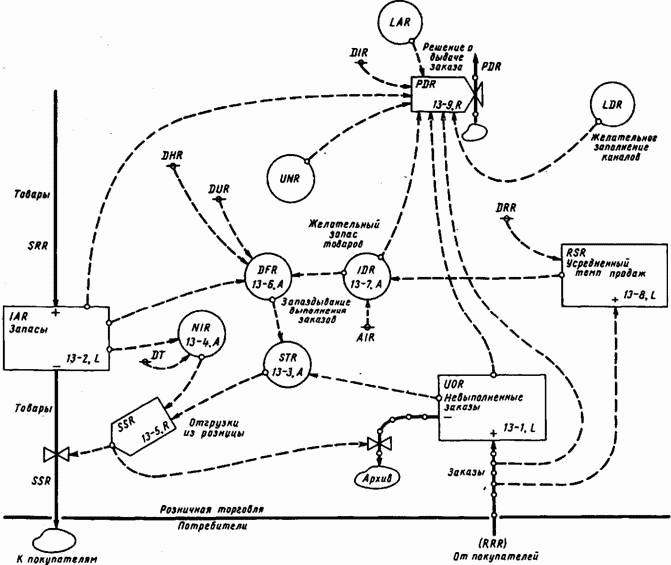
Рис. 13–13. Отражение решения о закупках в диаграмме потоков розничной торговли

Прежде всего темп розничных закупок будет зависеть от сложившегося темпа продаж RRR в течение предшествующего интервала времени JK[74]; это будут заказы, направленные на возобновление запаса товаров взамен проданных. Следует иметь в виду, что речь идет о предстоящем решении, которое принимается на основе самой последней достоверной информации, а запаздывание в процессе сбора информации должно быть введено позже.

Запаздывание DIR есть постоянная времени, отражающая тот темп, с каким розничная торговля в среднем реагирует на возникновение дефицита товаров в запасе и каналах системы. Нельзя предположить, что розничная торговля будет немедленно реагировать в полную силу на любую теоретически возможную разницу между желательным и фактическим запасами. Более того, потери времени на обнаружение такой разницы могут быть весьма существенными. Константа DIR позволяет установить это время реакции. К примеру, если величина DIR была бы равна 4 неделям, то темп пополнения запасов был бы таков, что любой остающийся дефицит (величина дефицита определяется выражением, стоящим в квадратных скобках) компенсировался бы со скоростью одной четверти дефицита в неделю. Позже мы увидим, что эта постоянная представляет собой один из решающих параметров, определяющих динамическое поведение системы.

Два члена уравнения, относящиеся к запасам, дают разницу между желательным и фактическим запасами. Если уровень желательного запаса будет выше или ниже фактического, то темп размещения заказов будет соответственно скорректирован.

Два члена уравнения, относящиеся к каналам системы, подобны членам уравнения, описывающим запасы. Желательный уровень заказов в каналах будет определен позднее (он пропорционален среднему уровню продажи товаров) тем же способом, что и желательный запас. В реальной обстановке вряд ли можно быть уверенным в том, что многие организации розничной торговли сознательно подходят к выдаче заказов, необходимых для заполнения каналов, как к части своих действий по размещению заказов. Если они этого не делают, то заказы, необходимые для сохранения желательного темпа поставки товаров, будут автоматически выдаваться за счет собственных запасов, так что принимаемые в это время меры с целью отрегулировать объем запасов приведут к размещению необходимого числа дополнительных заказов. Постоянная времени запаздывания DIR допускает изменение величины преднамеренного или непреднамеренного запаздывания в процессе регулирования.

Член приведенного уравнения UOR, обозначающий уровень не выполненных розничной торговлей заказов, включен в связи с общим стремлением получить уверенность в том, что уравнения останутся справедливыми и при экстремальных условиях деятельности системы. Если поставка товаров из производства отсутствует, а объем не выполненных розничной торговлей заказов столь велик, что побуждает покупателей воздерживаться от дальнейших закупок, в этом случае темп поступления розничных заказов RRR становится равным нулю. При таких обстоятельствах фактический уровень запасов будет снижаться до нуля. Согласно уравнениям 13-7 и 13-8, желательный уровень запасов при данных обстоятельствах будет также снижаться до нуля. Это может показаться на первый взгляд неправдоподобным; но на самом деле при отсутствии как поступающих заказов, так и поставок, и при наличии задолженности по невыполненным заказам представляется нежелательным и ненужным иметь запас товаров. При таких обстоятельствах важно, чтобы не выполненные розничной торговлей заказы получили отражение в объеме заказов, не выполненных оптовыми базами. Иначе в высших звеньях системы не окажется наличных заказов, чтобы возобновить поток товаров, когда сбыт вновь станет возможным. Как мы позже увидим, уровень находящихся в каналах заказов LAR включает задолженность по заказам, не выполненным оптовыми базами. Однако, если член, характеризующий объем невыполненных заказов, не будет включен в уравнение 13-9, то мы увидим, что не выполненные оптовыми базами заказы будут отменены и сойдут на нет. Это случится потому, что при отсутствии снабжения все другие члены уравнения могут стать равными нулю. Тогда выражение LAR, входящее в уравнение с отрицательным знаком и определяющее необходимое заполнение каналов, включая в этих условиях только задолженность по не выполненным оптовыми базами заказам, приведет к отрицательному значению темпа размещения заказов на все время, пока не будет ликвидирована задолженность в оптовой торговле. Положительный член уравнения UOR уравновешивает в этом случае отрицательный член LAR, так что задолженность по не выполненным оптовыми базами заказам сохраняется.

Выражение, описывающее нормальный для розничного торгового звена объем невыполненных заказов UNR, включено в уравнение таким образом, чтобы в условиях равновесия фактический запас в розничной торговле был равен желательному. При нормальных условиях равновесия два члена уравнения, относящиеся к каналам, взаимно погашаются; мы можем ожидать того же и в отношении двух членов, обозначающих запасы. Однако если бы член уравнения UOR, обозначающий объем невыполненных заказов, мог остаться в уравнении без корректирующего члена, отражающего нормальный уровень невыполненных заказов UNR, то члены, соответствующие запасам, должны были бы отличаться на величину, достаточную для того, чтобы это соответствовало объему невыполненных заказов UOR. Хотя можно подобрать такие значения для различных констант, определяющих запасы, при которых фактические запасы будут достигать желательного объема, было бы ошибкой и противоречило бы смыслу, который мы вкладываем в понятие «желательный запас», если бы фактическая величина запасов при стабильных условиях не стремилась бы стать равной их желательной величину

Неустановившееся взаимодействие между членами уравнения, характеризующими наличие запасов, заполнение каналов и объем невыполненных заказов имеет существенное значение. Предположим, что количество имеющихся товаров IAR меньше по сравнению с желательным их количеством IDR. Это вызовет определенный темп размещения заказов, которые будут учтены в члене уравнения LAR, отражающем заполнение каналов. Когда заказы будут размещены в необходимом количестве, то в связи с включением величины дополнительных заказов в отрицательный член LAR уравнения общая величина выражения, заключенного в уравнении 13-9 в скобки, уменьшится до нуля. При поступлении товаров, заказанных для пополнения запасов, они будут переходить из заказов в канале LAR в наличный запас IAR, так что уравнение заказов будет продолжать оставаться сбалансированным. Таким образом, уравнение отражает возможность избежать повторного заказа товаров для пополнения запаса в следующие за моментом заказа периоды времени до того, как будут поставлены требуемые товары.

К анализу членов уравнения 13-9, заключенных в скобки, можно подойти с другой точки зрения. Сгруппировав положительные члены уравнения (IDR.K+LDR.K+UOR.K), можно представить желательное наличие товаров в розничной торговле как сумму желательного запаса, необходимого количества транспортируемых по каналам системы товаров и числа изделий, предназначенных для выполнения имеющихся заказов. Этой сумме будет противопоставлена отрицательная сумма членов уравнения (IAR.K+LAR.K+UNR.K), которые отражают существующий в данный момент запас товаров, товары, находящиеся в настоящее время в каналах, и невыполненные заказы в объеме, признаваемом нормальным.

Темп закупок, определяемый с помощью уравнения 13-9, зависит от значений нескольких переменных, которые еще не определены. Это, в частности, желательный (или необходимый) уровень заказов и товаров, находящихся в движении по каналам, связывающим розничную и оптовую торговлю. Необходимое количество заказов и товаров в этих каналах будет зависеть от их длины (то есть от общего запаздывания) и от среднего уровня продаж в розничной торговле, который необходимо обеспечить; такую зависимость можно представить следующим уравнением:

,

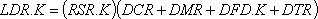13–10, А

где

LDR — желательный (или необходимый) для снабжения розничного звена уровень заказов в каналах (единицы);

RSR — усредненные требования к розничному звену (средний темп продаж) (единицы в неделю);

DCR — запаздывание оформления заказов в розничном звене (недели);

DMR — почтовое запаздывание отправленных из розничного звена заказов (недели);

DFD — запаздывание (переменное по величине) выполнения заказов оптовыми базами (недели);

DTR — запаздывание транспортировки товаров в розничное звено (недели).

Среднее суммарное число заказов и товаров LDR, которое должно находиться в движении по каналам, является результатом умножения среднего темпа продаж в секторе розничной торговли RSR на общее время, необходимое для совершения заказом полного кругооборота по каналам системы. Выражение в круглых скобках в правой части уравнения дает это общее запаздывание. Три составляющие этого запаздывания, связанные с оформлением заказов DCR, с доставкой заказа почтой DMR и с транспортировкой товаров DTR, являются величинами постоянными: в данном случае предполагается, что они не изменяются при изменении состояния изучаемой системы[75]. Запаздывание при выполнении заказов оптовыми базами DFD зависит от наличия запасов на этих базах, за счет которых могут быть выполнены заказы; оно является поэтому переменным по величине, как и аналогичное запаздывание в розничной торговле.

Фактическое содержимое каналов состоит из суммы заказов и товаров в различных участках каналов:

,

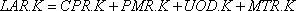13-11, А

где

LAR — фактический уровень выданных розничным звеном заказов, находящихся в каналах (единицы);

CPR — заказы в розничном звене на стадии оформления (единицы);

PMR — выданные розничным звеном заказы на закупки, находящиеся в почтовых каналах (единицы);

U0D — заказы, не выполненные оптовыми базами (единицы);

MTR — товары в пути к розничному звену (единицы).

Реальное количество, передаваемое по каналу, определяется в данном случае как вспомогательная переменная, равная сумме четырех уровней заказов и товаров, сложившихся на четырех участках канала.

Член уравнения 13-9, который нами еще не определен, — это нормальный уровень не выполненных розничной торговлей заказов UNR. Он равен среднему темпу продаж, умноженному на нормальное запаздывание выполнения заказов:

UNR.K=(RSR.K)(DHR+DUR),

13–12, A

где

UNR — нормальное для розничной торговли число невыполненных заказов (единицы);

RSR — усредненные требования к розничному звену, средний темп продаж (единицы в неделю);

DHR — минимальное запаздывание выполнения заказа розничным звеном (недели);

DUR — запаздывание выполнения заказов розничным звеном из-за отсутствия на складе некоторых товаров при нормальном общем объеме запасов (недели).

Нормальное запаздывание в розничной торговле состоит из двух компонентов — один представляет собой среднее минимальное время, необходимое для оформления документов, другой порожден обычными условиями отсутствия запасов некоторых видов товаров. Общее запаздывание, умноженное на средний темп продаж, дает «нормальное» ожидаемое число невыполненных заказов.

Уравнения с 13-1 по 13–12 полностью определяют уровни, темпы и вспомогательные переменные в розничной торговле, необходимые для составления уравнений темпов. Теперь надо составить уравнения, описывающие запаздывания. Рассмотрим три отдельных запаздывания — в размещении заказов, в пересылке заказов по почте из розничной торговли в оптовую и в доставке товаров с оптовых баз в розничную торговлю. На рис. 13–14 показана диаграмма потоков, дополненная уравнениями с 13–10 по 13–18 (включая запаздывания). Запаздывание выполнения заказов оптовой базой будет включено в диаграмму потоков позднее при описании оптовой торговли.

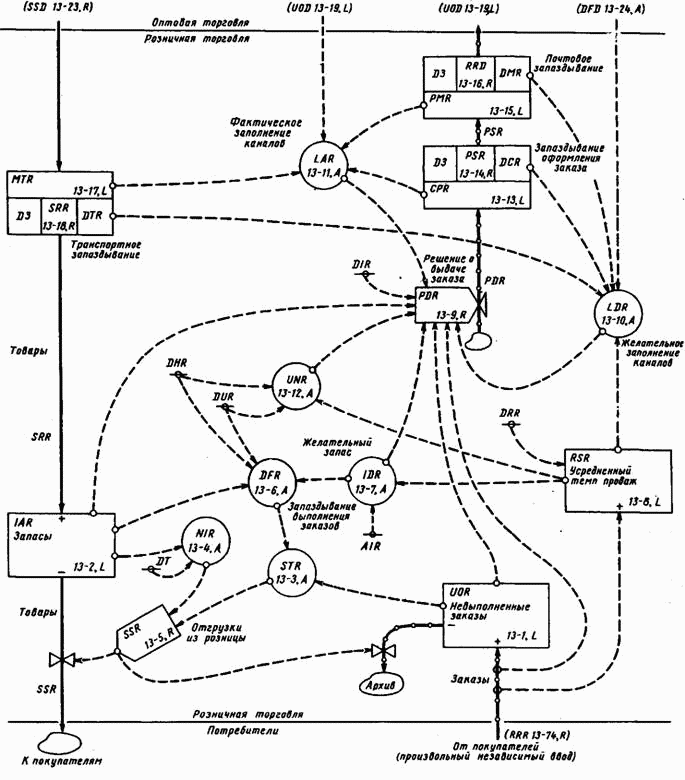
Рис. 13–14. Диаграмма потоков в розничной торговле.

Мы используем запаздывание третьего порядка как наиболее точно отображающее наше интуитивное «ощущение» того, каким образом процесс оформления заказов, пересылка их по почте и доставка товаров реагируют на различные установившиеся и неустановившиеся вводы[76]. Запишем два уравнения: одно из них (уравнение уровня) будет определять количество, находящееся в процессе транспортировки; другое, записанное в «стенографической» форме, будет указывать на способ вычисления темпа на выходе. При выполнении расчетов с помощью вычислительной машины «функциональное обозначение» этого темпа на выходе может быть автоматически преобразовано в необходимые уравнения темпов и уровней с помощью простой программы. Уравнение, используемое ниже для определения темпа на выходе из запаздывания, не является поэтому действительным разностным уравнением, которое может быть решено, а служит просто указанием вычислительной машине, какой метод вычислений следует применить. Детальные инструкции, заложенные в программу вычислительной машины, обеспечивают автоматическое получение реальных уравнений.

Два уравнения, определяющие запаздывание третьего порядка при принятии решения о закупке и размещении заказов розничной торговли в оптовой, имеют следующий вид:

CPR.K=CPR.J+(DT)(PDR.JK — PSR.JK),

13-13, L

PSR.KL=DELAY3(PDR.JK, DCR),

13–14, R

где

CPR — заказы в розничном звене в стадии оформления (единицы);

PDR — темп закупок розничным звеном, устанавливаемый в результате решения (единицы в неделю);

PSR — выданные розничным звеном заказы на закупку товаров (единицы в неделю);

DCR — запаздывание оформления заказа в розничном звене (недели);

DELAY3—функциональное обозначение (а не переменная), определяющее систему уравнений, описывающих запаздывание третьего порядка[77].

Уравнение 13–13 — это обычное уравнение уровня; уравнение 13–14 показывает, каким образом может быть определен темп на выходе. Следует заметить, что выражение DELAY3 не является переменной, как другие группы символов, а обозначает функциональную зависимость запаздывания третьего порядка от темпа на входе PDR и запаздывания DCR. Оно указывает, какие операции должны быть выполнены над величинами. В нем утверждается, что должно быть образовано запаздывание третьего порядка, в котором темп ввода есть переменная PDR, определяемая в соответствии со своим уравнением, а величина запаздывания задана константой DCR.

Выход из запаздывания, связанного с процессом оформления заказа, служит вводом для почтового запаздывания. Почтовые операции также будут отображены показательным запаздыванием третьего порядка:

PMR.K=PMR.J+(DT)(PSR.JK — RRD.JK),

13-15, L

RRD.KL=DELAY3(PSR.JK, DMR),

13–16, R

где

PMR — выданные розничным звеном заказы на закупки, находящиеся в почтовых каналах (единицы);

PSR — выдаваемые розничным звеном заказы на закупку товаров (единицы в неделю);

RRD — требования (заказы), получаемые оптовыми базами (единицы в неделю);

DMR — почтовые запаздывания заказов, отправленных из розничного звена оптовым базам (недели);

DELAY3— функциональное обозначение, указывающее на уравнения запаздывания третьего порядка.

Как и прежде, уравнение 13–15 определяет количество, перемещаемое в запаздывании. Функция DELAYS в уравнении 13–16 указывает, каким образом можно определить тот темп на выходе из почтового запаздывания, который и является действительным темпом получения заказов оптовыми базами.

Чтобы завершить описание розничной торговли, нужно отобразить в модели транспортировку товаров из оптовых баз в розничную торговлю. Для этой цели запишем еще два уравнения, характеризующие запаздывание при этой транспортировке:

MTR.K=MTR.J+(DT)(SSD.JK — SRR.JK),

13-17, L

SRR.KL=DELAY3 {SSD.JK, DTR),

13–18, R

где

MTR — товары в пути к розничному звену (единицы);

SSD — поставки, осуществленные из запасов оптовых баз (единицы в неделю);

SRR — поставки, пополнившие запасы розничной торговли (единицы в неделю);

DTR — запаздывание транспортировки товаров в розницу (недели);

DELAY3 — функциональное обозначение, указывающее на уравнения запаздывания третьего порядка.

Вводом в запаздывание транспортировки служит темп на выходе из запасов оптовой торговли. Выход SRR из запаздывания при поставке служит вводом в запасы товаров розничной торговли, как этого требует уравнение 13-2. Как и прежде, уравнение 13–17 определяет объем транспортируемых товаров, а уравнение 13–18 дает необходимые указания для вычисления темпа выхода в соответствии с характеристиками запаздывания третьего порядка.

Полученную совокупность систем уравнений мы предполагаем использовать для отображения в модели операций в розничной торговле. Эти уравнения не являются независимыми, поскольку в них входят некоторые переменные (SSD, UOD, DFD), относящиеся к оптовой торговле.