8. 4. Реакция показательных запаздываний

8. 4. Реакция показательных запаздываний

После того как мы рассмотрели математическую форму показательных запаздываний, целесообразно перейти к изучению их поведения. Характерной особенностью неустановившейся реакции запаздывания (то есть изменения темпа исходящего из запаздывания потока во времени) является ее изменение при увеличении числа секций первого порядка в запаздывании.

Рассмотрим прежде всего частный пример запаздывания, связанного с доставкой товаров с завода в оптовую торговую сеть. Неустановившуюся реакцию фактического реального процесса доставки можно лучше всего выявить, если представить себе поставки большого количества товаров на несколько оптовых баз, расположенных в разных местах, выполняемые с помощью различных видов транспорта. В момент, когда в транспортную систему одновременно вводится большое число единиц товаров, на входе в запаздывание, которое отражает эту систему, возникает «импульс»; наша задача заключается в определении темпа поступления товаров в пункты назначения.

Для этого примера среднее запаздывание могло бы быть установлено довольно просто, поскольку оно зависит от способа транспортировки и расстояний. Однако можно предполагать, что неустановившаяся реакция будет более сложной и потребует более внимательного рассмотрения.

Чтобы правильно представить неустановившуюся реакцию в данном примере, можно было бы сравнить предполагаемое поведение реальной системы с различными взятыми на выбор показательными запаздываниями. На рис. 8–3, 8–4, 8–5 и 8–6 показаны некоторые представители различных видов показательных запаздываний.

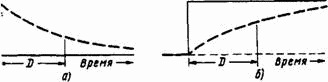
Рис. 8–3. Показательное запаздывание первого порядка.

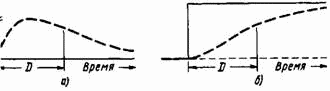
Рис. 8–4. Показательное запаздывание второго порядка.

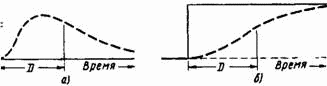
Рис. 8–5. Показательное запаздывание третьего порядка.

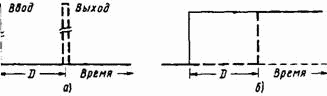
Рис. 8–6. Дискретное, или канальное, запаздывание.

На этих рисунках сплошная линия представляет ввод в запаздывание, пунктирная линия показывает выход. Время отложено по оси абсцисс. На каждом рисунке левая диаграмма построена для импульсного ввода, когда количество вводится в запаздывание в пренебрежимо малое время; пунктирная линия показывает темп появления этого количества на выходе. На правой диаграмме на вводе имеет место внезапное скачкообразное увеличение темпа ввода, а пунктирная линия снова показывает результирующий темп на выходе.

На рис. 8–3 представлено показательное запаздывание первого порядка. На рис. 8–3 а максимальный темп на выходе возникает немедленно после импульсного ввода, и после этого темп на выходе снижается по показательной кривой. Ясно, что эта кривая не характерна для запаздываний, связанных с поставкой товаров в рассматриваемом примере, поскольку рис. 8–3 а показывает, что максимальный темп поступления транспортируемых количеств в пункты назначения имеет место в момент, когда эти количества только вводятся в транспортную сеть. Конечно, максимальный темп поступления не может иметь места в этот момент.

Рис. 8–3 б показывает скачкообразное изменение в темпе ввода и результирующее увеличение темпа выхода из запаздывания первого порядка, которое описывается показательной кривой. Площадь между сплошной и пунктирной кривыми является мерой количества, накапливающегося в процессе транспортировки в запаздывании. Пока через запаздывание проходит поток, общее количество, поступающее на выход, меньше общего введенного в запаздывание количества на величину, находящуюся в процессе транспортировки.

На рис. 8–4 показана реакция на выходе показательного запаздывания второго порядка. Это запаздывание эквивалентно двум запаздываниям первого порядка, расположенным друг за другом так, что выход первого служит входом второго. На рис. 8–4 а начальный темп выхода как реакция на импульсный ввод равен нулю, а кривая выхода имеет максимальную крутизну в начальной своей части. Это также, по существу, неприемлемо, если говорить о запаздываниях при поставках, поскольку нельзя ожидать, что темп поступления начинает резко возрастать в момент, когда отгруженные товары покидают предприятие.

На рис. 8–5 изображено показательное запаздывание третьего порядка. Такая форма реакции на выходе в отличие от рассмотренных ранее удовлетворяет очевидным характеристикам фактического процесса поставки. На рис. 8–5 а выходная реакция на импульсный ввод вначале равна нулю; при этом угол наклона кривой выхода в начальной точке также равен нулю. Кривая начинает медленно подниматься, достигает максимальной крутизны, а затем и экстремального значения, и идет вниз. На рис. 8–5 б показан выход, следующий за скачкообразным изменением в темпе ввода.

Запаздывание третьего порядка удовлетворяет важнейшим требованиям, которые мы можем интуитивно предъявить к выражающей его функции в приведенном выше примере доставки товаров. Дальнейшее уточнение функции запаздывания потребовало бы тщательного изучения каждого из запаздываний в реальной системе и их распределения во времени. Маловероятно, что какое-либо дальнейшее уточнение будет оказывать заметное влияние на поведение системы.

Если показательное запаздывание постоянной общей продолжительности дробить на увеличивающееся число последовательных секций первого порядка все меньшей и меньшей величины, то начальное запаздывание в ответ на импульс увеличивается, прежде чем возникает реакция на выходе. При этом подъем кривой выхода происходит круче, круче становится и спад этой кривой; в результате нулевое значение темпа на выходе наступает быстрее. Последний, конечный член этой группы запаздываний представляет собой гипотетическое запаздывание неопределенного порядка[44]. Его иногда называют дискретным, или канальным, запаздыванием. Рис. 8–6 дает представление о показательном запаздывании неопределенного порядка, где на выходе ничего не происходит до тех пор, пока не пройдет время запаздывания D; после этого на выходе сразу же в точности воспроизводится ввод. На рис. 8–6 а показан импульсный ввод определенного количества в запаздывание и, как результат, импульсный выход, возникающий в момент времени D. Рис. 8–6 б показывает реакцию на скачкообразное изменение темпа ввода. Темп ввода возрастает внезапно от нуля до конечной величины реакции; то же происходит и на выходе на D дней позже. Ясно, что такое представление запаздывания не будет правильно отражать реальную обстановку в приведенном выше примере, поскольку в этом случае оказалось бы, что все поставки, которые были начаты в один и тот же момент, должны быть выполнены точно в одно и то же время, на D дней позже, независимо от того, насколько далекой была транспортировка.

При отображении запаздывания, связанного с установлением темпа производства на предприятии после его реконструкции, у нас может появиться желание получить более длительное начальное запаздывание, чем создающееся в случае с показательным запаздыванием третьего порядка. Так как последовательное расположение показательных запаздываний увеличивает начальное запаздывание и крутизну восходящей ветви кривой, то в этом случае можно будет воспользоваться, например, запаздыванием шестого порядка (то есть двумя последовательными запаздываниями третьего порядка).

После того как будет найдена функциональная форма, качественно соответствующая накопленному нами знанию фактов, отпадет необходимость в соответствующих данных для дальнейшего уточнения функции. Это положение может служить иллюстрацией общих соображений в разделе 3.7 об источниках информации для разработки моделей. Как только удастся установить вид функции, которая качественно удовлетворяет характеристикам реальной системы, как в неустановившихся, так и в стабилизированных условиях, лучше всего, вероятно, перейти к другим частям модели, пока испытания сами не выявят ее чувствительности к некоторым принятым допущениям[45].

На рис. 8–7 показаны реакции на выходе запаздываний, выраженных показательной функцией первого, второго, третьего, шестого и неопределенного порядков для случая, когда ввод является импульсным. Это значит, что в нулевой момент времени в запаздывание вводится определенное количество и на этом ввод прекращается. Проследим за темпом на выходе. По оси абсцисс на рис. 8–8 отложено время в единицах общего среднего запаздывания D, которое определяется таким образом, чтобы при установившемся потоке его темп, умноженный на величину среднего запаздывания, определил находящееся в нем количество содержимого. Другими словами, все кривые приведены к одинаковым условиям таким образом, что для запаздывания величиной D и для постоянного потока через запаздывание в количестве R единиц в единицу времени, количество предметов, находящихся в процессе продвижения, было равно произведению (R)(D).

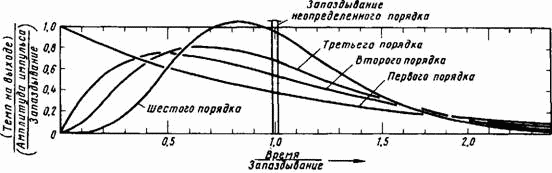
Рис. 8–7. Реакции показательного запаздывания на единичный импульс.

Нетрудно заметить, что запаздывание п-го порядка эквивалентно п последовательным запаздываниям первого порядка, каждое из которых имеет продолжительность D/n. В установившемся потоке каждое запаздывание первого порядка имеет одинаковый темп потока и, следовательно, заключает в себе 1/n-ю часть общего количества единиц, имеющихся в запаздывании.

По оси ординат на рис. 8–7 отложен темп потока на выходе, отнесенный к начальному темпу запаздывания первого порядка, который равен I/D, где I есть количество, вводимое в начальный момент в виде импульса, a D есть среднее запаздывание. Отношение I/D имеет размерность единицы/время.

На рис. 8–8 показан выход из запаздываний первого, второго, третьего, шестого и неопределенного порядков при скачкообразном характере изменения темпа ввода; в этом случае в нулевой момент времени задается величина темпа внезапно возникшего потока на входе. По оси ординат на этом рисунке отложено отношение темпа потока на выходе из запаздывания к темпу на входе[46].

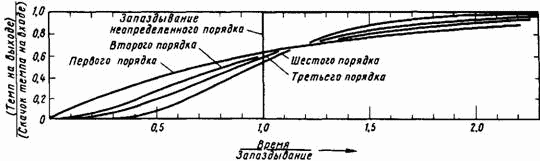
Рис 8–8. Реакции показательного запаздывания на скачкообразное изменение темпа на входе.