Приложение A ИНТЕРВАЛ РЕШЕНИЯ УРАВНЕНИЙ

Приложение A

ИНТЕРВАЛ РЕШЕНИЯ УРАВНЕНИЙ

В разделе 6.5 рассмотрены правила выбора интервала DT при решении уравнений модели динамической системы. Следовало бы вновь прочесть этот раздел, прежде чем переходить к настоящему приложению.

Выбор интервала зависит от взаимоотношений уровней и темпов потоков в системе. Уровни взаимосвязаны с входящими и исходящими потоками через среднюю величину запаздывания, которое они испытывают в данном уровне. Такое суждение правильно в отношении всех уровней, а не только тех, которые проявляются в формах, называемых нами запаздываниями. Когда интервал решения становится слишком большим, содержимое уровня может оказаться сравнимым с тем количеством, которое поступает или исходит из уровня в течение данного интервала времени. Если это случается, то либо интервал решения слишком продолжителен, либо уровень, о котором идет речь, потерял свое значение в системе и может быть опущен из рассмотрения (почтовые запаздывания не учитывались при рассмотрении модели производственно-сбытовой системы в главе 13).

Влияние изменения интервала решения можно проследить, рассмотрев уравнения запаздываний первого порядка (см. главу 8, уравнения 8–1 и 8–2).

LEV.K = LEV.J+(DT)(IN.JK-OUT.JK)

.

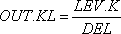Предположим, что запаздывание вначале отсутствует; при этом темпы входящего и исходящего потоков равны нулю; скачок темпа входящего потока в одну единицу за единицу времени имеет место в момент времени, равный нулю. На рис. A-1 показаны итоговые кривые при различных отношениях величины интервала решения ко времени запаздывания, DT/DEL. По горизонтальной оси отложена отвлеченная величина отношения времени к величине запаздывания DEL.

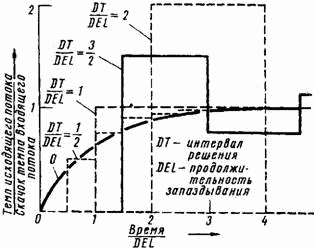
Рис. A-1. Реакция запаздывания первого порядка на ступенчатый ввод при различных отношениях интервала решения DT к запаздыванию DEL.

Если интервал решения пренебрежимо мал, то практически в результате получается экспоненциальная кривая, показанная на графике для интервала, равного 0. Когда DT составляет половину от DEL, то в первой расчетной точке уровень, как и величина выходного темпа, достигает половины своего конечного значения. Остающаяся разница между выходными и входными темпами сокращается за каждый интервал времени наполовину.

Если интервал решения равен времени запаздывания, то уровень и темп исходящего потока достигают своих конечных величин к моменту окончания первого этапа вычислений. Экспоненциальное запаздывание приобретает некоторые черты, характерные для запаздывания в каналах снабжения. (Однако таким способом нельзя определять общее запаздывание в каналах снабжения.)

Для еще больших интервалов решений первый вычисленный уровень (как для кривой при DT=³/₂ времени запаздывания) превысит его установившуюся величину. Темп выхода превысит темп входа. На следующем этапе вычислений величина уровня получится меньше своего установившегося значения. Если интервал решения находится между DEL и 2 (DEL), то в кривой выхода возникнут затухающие колебания.

При DT, равном 2 (DEL), при появлении скачка на входе на выходе возникнут незатухающие колебания. Если интервал решения DT больше, чем 2 (DEL), то колебания на выходе величины будут непрерывно возрастающими.

Кривая на рис. А-1 для интервала решения, равного половине постоянной запаздывания, вероятно, является приемлемым приближением, если только некоторые из запаздываний в системе приблизятся к выбранному значению интервала решения.

Следует иметь в виду, что запаздывание третьего порядка состоит из трех запаздываний первого порядка. Если для каждого из них принимать отношение DTIDEL — ¹/₂, то интервал решения в этом случае должен быть равен или меньше ¹/₆ от постоянной времени запаздывания любого экспоненциального запаздывания третьего порядка.

Критерий, использованный здесь для выбора интервала решения, обусловлен структурой системы и ее внутренними динамическими свойствами. Выбор величины интервала между вычислениями в модели нельзя связывать с таким фактором, как периодичность, с которой возможен сбор информации в моделируемой реальной системе. Интервалы решения, выбранные по предложенной здесь методике, будут гораздо короче тех, которые упоминались в литературе по экономическим моделям, и иногда составляли год, даже тогда, когда изучались кратковременные ежегодные изменения в системе.

Влияние величины интервала решения может быть определено эмпирически, с помощью ряда проигрываний модели с тем, чтобы выяснить, в какой мере величина интервала решения сказывается на результатах. Это было сделано на модели (рис. 15-9) фирмы, выпускающей детали электронного оборудования с учетом ранее применявшихся методов управления при величине TBLAF, равной 40 неделям. Результаты приведены на рис. A-2.

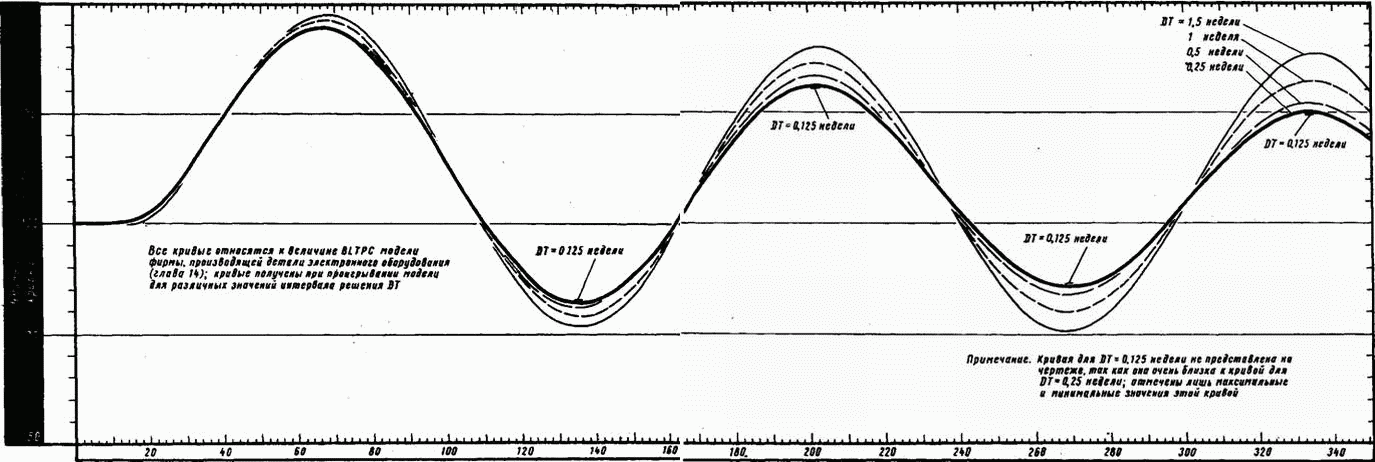
Рис. А-2. Влияние изменения интервала решения.

Проигрывания проводились при величине интервала DT, равной 0,125 недели, 0,25 (как и в главе 15), 0,5, 1,0, 1,5 и 2,0 недели. Величины, полученные при интервалах DT в 0,125 недели и 0,25 недели, настолько близки друг к другу, что их трудно различить на графиках. Проигрывание для DT, равного 2,0 недели, в числовом отношении было неустойчивым, и на 76-й неделе величины превысили значения, допускаемые разрядностью регистров вычислительной машины.

Этот конкретный анализ с помощью счетно-решающего устройства должен быть особенно чувствителен к влиянию величины интервала решения, так как была использована ступенчатая входная функция, а колебание системы было «свободно протекающим», без наличия управляющей функции для регулирования периодичности. Даже при таком условии время наступления третьего максимума заключено в пределах одной, 335-й недели для каждой из кривых.

Величина амплитуды при различных интервалах решения изменяется несколько больше, чем период колебаний; относительные величины амплитуды после двух полных периодов колебаний приведены в табл. А-1.

Таблица A-1. Влияние интервалов решений на амплитуду колебаний

Отношение третьего максимума к первому составляет 0,79 для интервала решения в 0,125 недели, 0,85 — для интервала в 1,0 недели и 0,90 — для интервала в 1,5 недели. Эти различия несущественны по сравнению с теми изменениями результатов в различных условиях, которые наблюдались в главе 15.

Некоторые постоянные времени в модели главы 14 (DCPF, DMBLF и DSF) равны 1 неделе, то есть они меньше самого большого интервала решений в табл. А-1. Как видно из таблицы, ошибка в вычислении начинает довольно быстро увеличиваться. При интервале решения в 2 недели некоторые типы внутренних взаимодействий приводят к неустойчивому решению. Зависимость между интервалом решения и величиной третьего максимума кривой невыполненных заказов BLTPC графически представлена на рис. A-3. Величина BUT PC измеряется в процентах от ее первоначального значения.

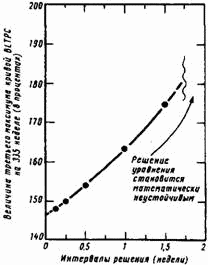
Рис. A-З. Результаты расчета в зависимости от величины интервала решения.

Изложенное свидетельствует о том, что обычно можно выбирать интервал решений DT, равный или меньший 0,5 недели (меньше половины самого короткого времени запаздывания первого порядка, в данном случае равного 1 неделе для DCPF, DMBLF и DSF). Такой выбор величины DT дает численные результаты, незначительно отличающиеся от тех, которые получились бы при меньшей величине DT (см. рис. А-2).