6. 4. Классы уравнений

6. 4. Классы уравнений

Уравнения уровней и темпов уже рассматривались при описании основных свойств используемой ниже структуры динамической модели.

Были перечислены и другие типы уравнений, которыми удобно пользоваться, но которые не вносят в модель новых динамических характеристик. Это вспомогательные и дополнительные уравнения и уравнения начальных условий. Рассмотрим форму этих уравнений.

Уравнения уровней. Уровни представляют собой переменное по величине содержимое резервуаров в системе. Как уже отмечалось, они существовали бы и в том случае, если бы система была приведена в состояние покоя и все потоки в ней остановились бы. Значения уровней определяются заново для каждого из последующих интервалов решений; предполагается, что между моментами времени, для которых решаются уравнения, уровни изменяются с постоянной скоростью, но их значения в этом промежутке времени не вычисляются.

Вот пример типичного уравнения уровня:

.

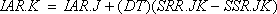6–1, L

Символы обозначают следующие переменные:

IAR — фактический запас товаров в розничной торговой сети (единицы), где слово «фактический» употребляется в отличие от «требуемый» и других понятий о запасе товаров;

DT — приращение времени (недели), интервал времени между решениями системы уравнений;

SRR — поставки товаров в розничную торговую сеть (единицы в неделю);

SSR — продажа товаров в розничной торговой сети (единицы в неделю)[33].

Обозначение «6–1, L» справа указывает, что данное уравнение является первым в главе 6 (всем уравнениям присвоен цифровой шифр) и что оно описывает уровень («L»)[34].

Уравнение устанавливает прямую количественную зависимость, согласно которой запас товаров 1AR в момент времени К будет равен предыдущему значению IAR.J плюс произведение разности между темпами входящего потока SRR.JK и исходящего потока SSR.JK на продолжительность интервала времени DT, в течение которого существуют эти темпы. Короче говоря, то, что есть в торговой сети, равно тому, что в ней было, плюс то, что поступило, и минус то, что было из нее отдано[35].

Следует заметить, что все члены уравнения имеют размерность «единицы» товаров. В скобках правой части уравнения «единицы» получаются при умножении времени, выраженного в долях недели, на темпы потока в единицах в неделю.

Темпы потока всегда измеряются числом единиц за какой-либо интервал времени, такой, как день, неделя или месяц, но не в периодах, кратных интервалу решений DT; единицы времени для темпов и интервала DT должны быть одними и теми же, например недели или месяцы. Уравнение сохраняет силу и не зависит от интервала решений DT, пока интервал не превышает максимальной величины, которая будет рассмотрена ниже. При изменении интервала решений не требуется вносить изменения в формулировку уравнения или в какие-либо входящие в него константы. Вводя интервал DT непосредственно в уравнение мы можем использовать в модели те же общепринятые единицы измерения времени, что и в реальной системе.

Сравнения уровней не зависят одно от другого; решение каждого из них зависит только от информации, касающейся предшествующего момента времени. Поэтому порядок решения уравнений уровней не имеет никакого значения. При решении какого-либо уравнения уровня в момент времени К не используется никакой информации из других уравнений уровней, решаемых для того же момента времени. Уровень в момент К зависит от его предыдущего значения в момент У и от темпов потока в течение интервала

Переменные, относимые к классу уровней, могут иметь такие единицы измерения, как «единицы в неделю», так что поначалу может показаться, что мы имеем дело с темпами. Тогда следует применить испытание системы приведением ее в состояние покоя, как это было сделано в разделе 5.1, где мы установили, что средние темпы представляют собой по существу уровни, а не темпы.

Уравнения темпов (функции решений). Уравнения темпов определяют темпы потоков между уровнями в системе. Уравнения темпов являются «функциями решений», что будет подробно рассмотрено ниже, в главе 9.

Уравнение темпа решается на основе данных о существующих в настоящее время величинах уровней в системе, которые часто включают в себя уровень, из которого исходит поток с данным темпом, и тот уровень, к которому он направлен. В свою очередь темпы потоков являются причиной изменений в уровнях. Уравнения темпов могут по типу решений относиться к «явным» или «неявным»[36]. Какая-либо разница в структуре самих уравнений при этом отсутствует.

В отношении уравнений темпов важно отметить, что они регулируют действия, которые должны произойти в системе за следующий интервал времени. В момент времени К уравнение темпа решается, чтобы определить то действие, которое будет управлять темпом потока в течение предстоящего интервала времени KL. В принципе уравнения темпов зависят только от значений уровней в момент времени К[37]. (На практике темпы, относящиеся к последнему, только что закончившемуся интервалу времени JK, могут иногда с достаточной степенью точности использоваться вместо уровня, характеризующего средний темп, в том случае, когда усреднение производится для очень короткого интервала времени.)

Уравнения темпов, как и уравнения уровней, на протяжении каждого интервала времени решаются независимо одно от другого. Взаимодействие в системе происходит при последующем воздействии темпов на уровни, которые затем в свою очередь оказывают влияние на темпы в более поздние интервалы времени. Уравнение темпа определяет действие, которое будет совершаться непосредственно в следующий момент. Если момент действия существенно близок (то есть продолжительность интервала решений DT существенно мала), то очевидно, что решение не может испытывать на себе влияния других решений, принимаемых в тот же момент времени в других частях системы[38]. Поэтому уравнения темпов независимы друг от друга и могут решаться в любой последовательности. Поскольку они зависят от значений уровней, вся группа уравнений темпов решается после того, как решены уравнения уровней.

Примером уравнения темпа может служить уравнение запаздывания исходящего потока, имеющее вид показательной функции первого порядка. Объяснение уравнения будет дано в главе 8, здесь же мы рассмотрим лишь его форму:

,

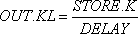6.2, R

где

OUT — темп исходящего потока (единицы в неделю);

STORE — количество, находящееся в настоящее время в запаздывании (единицы);

DELAY — константа, средняя продолжительность времени, необходимого для преодоления запаздывания (недели).

Это второе наше уравнение представляет собой уравнение темпа, о чем свидетельствует буква «R» в его шифре. Уравнение определяет величину темпа «OUT» и показывает, какое значение он будет иметь на протяжении следующего интервала времени KL. Темп должен быть равен величине уровня «STORE» в настоящий момент К, деленной на константу, названную «DELAY» (без какого-либо обозначения времени, поскольку это константа). Ко времени решения уравнения количественные значения для STORE и DELAY должны быть, конечно, известными.

Вспомогательные уравнения. Уравнение темпа может нередко стать очень сложным, если его действительно формулировать лишь на основе одних уровней, как это утверждалось до сих пор. К тому же темп может быть часто лучше определен, если пользоваться одним или несколькими понятиями, имеющими самостоятельный смысл и характеризуемыми в свою очередь уровнями системы. Часто бывает удобно разбить уравнение темпа на отдельные части, которые мы будем называть вспомогательными уравнениями. Вспомогательное уравнение оказывает большую помощь при решении задачи приведения модели в полное соответствие с действительной системой, так как с его помощью можно определить в отдельности многие факторы, принимаемые в расчет при выработке решения.

Вспомогательные уравнения являются промежуточными; они могут быть подставлены одно в другое (если имеется несколько «слоев» вспомогательных уравнений) и далее — в уравнения темпов[39]. Путем алгебраической подстановки вспомогательные переменные могут быть исключены из уравнений, что достигается ценой увеличения сложности уравнений темпов и потери в то же время простоты и ясности значения отдельных уравнений модели.

Вспомогательные уравнения решаются на момент времени К после решения уравнений уровней, поскольку для решения вспомогательных уравнений, как и для решения уравнений темпов, часть которых они собой представляют, используются данные о значениях уровней в тот же момент времени. Они должны быть решены прежде уравнений темпов, поскольку получаемые при этом результаты необходимы для подстановки в уравнения темпов.

В отличие от уравнений темпов и уровней вспомогательные уравнения нельзя решать в произвольной последовательности, так как одни вспомогательные уравнения могут быть составными частями других, а два или более вспомогательных уравнений могут образовывать «цепочку», которая должна решаться в определенном порядке таким образом, чтобы решение одного уравнения могло быть использовано при решении последующих. Если формулировка уравнений правильна, то должна существовать возможность такой последовательной подстановки. Система вспомогательных уравнений не должна быть замкнутой; это указывало бы на недопустимую и ненужную формулировку уравнений.

Ниже показана цепь из двух вспомогательных уравнений между двумя уровнями и уравнением темпа:

,

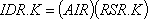6-3, A

где RSR — уровень, a AIR — константа,

,

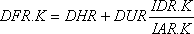6–4, А

где IAR — уровень, a DHR и DUR — константы,

,

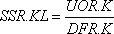6-5, R

где UOR — уровень.

Следует заметить, что в уравнении 6–3, А (индекс «A» применяется в шифре вспомогательных уравнений) уровень RSR в момент времени К используется в качестве ввода для вспомогательной переменной IDR в момент времени К-Выражения AIR, DHR и DUR — константы. В тот же момент времени К, IDR является вместе с другим уровнем вводом для вспомогательной переменной DFR. В свою очередь DFR используется вместе с другим уровнем в уравнении темпа 6–5,R для определения темпа SSR.

Отметим, что уравнение 6–3 может быть подставлено в уравнение 6–4 и далее в уравнение 6–5; тогда получим:

.

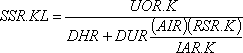6-6, R

Таким образом, могут быть исключены вспомогательные уравнения, а темп выражен только через уровни и константы.

В главе 13 уравнения 6–3, 6–4 и 6–5 рассматриваются применительно к обстановке на промышленном предприятии. Каждое из этих вспомогательных уравнений определяет имеющую самостоятельный смысл переменную, важную для отражения системы. Наши представления о системе были бы безнадежно затемнены, если бы мы действительно производили подстановку, выполненную в уравнении 6–6.

Вспомогательная переменная в принципе зависит только от уже известных уровней и от других вспомогательных переменных, значения которых могут быть вычислены до того, как они понадобятся. Как отмечалось в отношении уравнений темпов, значения темпов, относящиеся к предшествующему интервалу времени JK, могут быть иногда использованы во вспомогательных уравнениях; хотя это, строго говоря, неверно, однако при определенных условиях такой метод может дать достаточно хорошее приближение к средним значениям, получаемым для коротких интервалов времени.

Дополнительные уравнения. Дополнительные уравнения применяются при определении переменных, не являющихся частью структуры модели, но используемых при печати и графическом изображении величин, представляющих интерес для понимания поведения модели. Мы можем пожелать собрать информацию (например, о сумме запасов в целой системе), которая не используется в процессе выработки какого-либо решения в модели. Обозначение «S» указывает на дополнительное уравнение.

Уравнения начальных условий. Уравнения начальных условий используются для определения исходных значений всех уровней (и некоторых темпов), которое должно быть произведено до начала первого цикла решения уравнений. Они также используются в начальный момент времени для вычисления значений одних констант, исходя из значений других. Уравнения начальных условий решаются только один раз перед началом каждого проигрывания модели. Обозначение «N» указывает на уравнение начальных условий.