D. 2. Альтернативные уравнения для экспоненциальных запаздываний

D. 2. Альтернативные уравнения для экспоненциальных запаздываний

Разностные уравнения типа D-1 и D-2 могут быть записаны в различных формах. Форма записи, данная в разделе D-1, несколько неудобна, поскольку она требует суммирования двух количеств LEV и OUT при переходе от одного момента времени к следующему. В принципе, при таком переходе экспоненциальное запаздывание первого порядка должно бы требовать определения только одной числовой величины.

Для отображения экспоненциального запаздывания третьего порядка разработанная нами программа-компилятор использует одно уравнение для каждой ступени запаздывания первого порядка, которое может быть получено исходя из следующих соображений. Запишем уравнение D-2 для периода времени, предшествующего данному моменту времени К, при постоянном запаздывании:

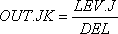
или

LEV.J = (DEL)(OUT.JK).

Подставив полученное выражение в уравнение D-1 и затем в D-2, после преобразований получим следующее уравнение:

.

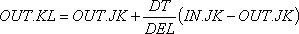Это уравнение имеет ту же форму, что и уравнение выравнивания, за исключением того, что оно определяет новую величину темпа исходящего потока на основании нового значения темпа входящего потока и прежнего значения темпа потока на выходе. Три уравнения такого вида определяют экспоненциальное запаздывание третьего порядка. Исходящий поток, согласно первому уравнению, определяет переменную, которая является вводом для второго уравнения, а определенная по этому уравнению исходящая величина становится вводом для третьего уравнения. Исходящий поток, определяемый третьим уравнением, является исходящим потоком запаздывания в целом. В этом случае каждое звено содержит ¹/₃ общего запаздывания.