Коэффициент Шарпа

Поскольку существует прямая положительная связь доходности и риска, очень удобными являются показатели, максимизация которых позволяет решать одновременно две задачи – максимизацию доходности и снижение риска. На интервале тестирования стратегии разработчик получает выборку из N значений доходности. Чем ближе элементы выборки друг к другу, и, следовательно, к их среднему значению, тем ровнее и стабильнее выглядит кривая роста капитала. Стремление к одновременной максимизации средней доходности и минимизации стандартного отклонения доходностей реализуется путем использования коэффициента Шарпа, широко применяемого практически во всех системах бэктестинга.

В оригинале коэффициент Шарпа выглядит как отношение между математическим ожиданием доходности и ее стандартным отклонением. Причем доходность измеряется за вычетом некой базовой доходности, например ставки безрискового актива. Мы предпочитаем использовать более практичный вариант коэффициента, пренебрегающий базовой доходностью (использование базовой доходности лишь усложняет вычисления, не принося дополнительной пользы при выборе наилучшей стратегии).

Коэффициент Шарпа для оценки стратегии в системе бэктестинга будем оценивать как SR = r/?, где r – средняя доходность серии из N доходностей, ? – среднеквадратичное отклонение этих доходностей. В экспоненциальном случае мы применяем среднюю геометрическую доходность (r^e), а в линейном случае – среднюю арифметическую доходность (r^l). Среднеквадратичное отклонение вычисляется по стандартной формуле

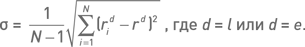
В итоге получается безразмерный показатель, не зависящий от длительности периода бэктестинга. На наш взгляд, коэффициент Шарпа – это один из самых удобных показателей бэктестинга.

Главным недостатком коэффициента Шарпа является то, что в нем никак не учитывается порядок, в котором чередуются прибыльные и убыточные месяцы. Из формул, применяемых для его вычисления, видно, что мы можем перемешать слагаемые в любом порядке без изменения результата. Это значит, что один и тот же коэффициент Шарпа может быть как у стратегии с равномерно растущим капиталом, так и у стратегии с неприемлемой величиной максимальной просадки. В хорошей стратегии не должно быть больших последовательностей следующих друг за другом убыточных месяцев. Эта проблема решается совместным использованием коэффициента Шарпа и описанных выше показателей риска (в частности, максимальной просадки).