Показатели доходности
Будем рассматривать два вида доходности, соответствующих двум подходам к управлению капиталом (имеется ввиду первый уровень системы управления капиталом, см. главу 4), – с постоянной суммой, инвестируемой в стратегию в каждый период времени, и с реинвестицией.
Первый подход удобен для анализа среднего результата серии однотипных портфелей. Этот случай хорошо подходит для стратегии, основанной на продаже волатильности незадолго до экспирации, когда каждая экспирации порождает один отдельный портфель. При этом для каждого элементарного периода времени используется одна и та же сумма E0. Для случая управления капиталом с постоянной суммой инвестиций будем пользоваться линейной годовой доходностью:
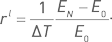
Эта величина соответствует средней арифметической доходности указанной серии, приведенной к годовому масштабу.
Второй подход к управлению капиталом более удобен для сравнения результатов стратегии с эталонным доходом типа непрерывно начисляемой процентной ставки (например, безрискового актива) или с определенным индексом (например, S&P 500). В таком случае следует пользоваться экспоненциальной годовой доходностью:
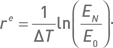
Экспоненциальная доходность соответствует средней геометрической доходности, приведенной к годовому масштабу.
Моменты времени, когда производятся измерения капитала, будем связывать с моментами экспирации опционов. В этом случае мы приходим к серии месячных прибылей и убытков. Пусть N – число месяцев в периоде, на котором производится бэктестинг стратегии. В линейном случае предполагается, что стартовый капитал каждого месяца равен Ei?1, а инвестируемый капитал всегда равен E0. Тогда прибыль i-го месяца pli = Ei ? Ei?1, средняя прибыль за месяц  средняя доходность
средняя доходность 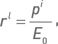 доходность i-го месяца
доходность i-го месяца  В экспоненциальном случае стартовый и инвестируемый капиталы для каждого месяца совпадают с конечным капиталом предыдущего месяца. О средней месячной прибыли говорить не имеет смысла, поскольку в каждом месяце инвестируется разная сумма. Доходность i-го месяца
В экспоненциальном случае стартовый и инвестируемый капиталы для каждого месяца совпадают с конечным капиталом предыдущего месяца. О средней месячной прибыли говорить не имеет смысла, поскольку в каждом месяце инвестируется разная сумма. Доходность i-го месяца  в качестве средней доходности экспоненциального случая разумно принимать среднюю геометрическую доходность
в качестве средней доходности экспоненциального случая разумно принимать среднюю геометрическую доходность 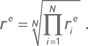
Для наборов {pl1, pl2…, plN}, {rl1, rl2…, rlN} и {re1, re2…, reN} можно рассчитать простые статистики, имеющие непосредственное значение для оценки стратегии инвестором. Максимальная месячная прибыль 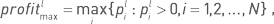 максимальная линейная месячная доходность
максимальная линейная месячная доходность 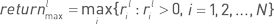 и максимальная экспоненциальная месячная доходность
и максимальная экспоненциальная месячная доходность 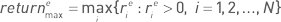 характеризуют один наиболее удачный месяц.
характеризуют один наиболее удачный месяц.
Противоположные по смыслу величины – максимальный месячный убыток в абсолютном и относительном (аналогично доходности) измерении – имеют большое значение, поскольку размеры этих величин могут оказаться неприемлемыми, и тогда такой вариант стратегии придется отвергнуть. Даже высокодоходная стратегия, имеющая на длительном интервале всего один убыточный месяц, может быть отвергнута, если этот убыток превышает определенную пороговую величину. Максимальный месячный убыток в абсолютном выражении имеет смысл только в линейном случае и определяется как 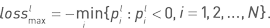 Аналогично определяются относительные величины для линейного случая как
Аналогично определяются относительные величины для линейного случая как  и для экспоненциального случая как
и для экспоненциального случая как 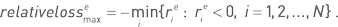
Общепринятым показателем риска является стандартное отклонение доходностей, зафиксированных на интервале ?. Чаще всего данный показатель рассматривается не сам по себе, а в совокупности со средней доходностью (см. ниже раздел, посвященный коэффициенту Шарпа).
Несложно также ввести и другие показатели: число прибыльных месяцев, число убыточных месяцев, средняя прибыль прибыльных месяцев, средний убыток убыточных месяцев, максимальное число прибыльных месяцев подряд, максимальное число убыточных месяцев подряд и т. п.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК