4.4.3. Трансформации весовой функции
Во всех рассмотренных выше примерах весовая функция ?(C) вычислялась для каждой комбинации C по значениям того или иного показателя, рассчитанного для этой комбинации. Говоря формальным языком, ?(C) это сложная функция вида ?(C) = f(x(C)), где x(C) – определенный показатель, выбранный для распределения капитала. До сих пор мы полагали, что весовая функция принимает значения показателя, то есть рассматривали частный случай ?(C) = x(C). В этом случае вес каждой комбинации в составе портфеля прямо пропорционален значению показателя, соответствующего данной комбинации (графически зависимость веса от показателя является прямой линией). Однако мы не обязаны ограничиваться частным случаем линейной зависимости и можем допустить в принципе любой вид весовой функции, соответствующий торговой идее и параметрам стратегии.
Например, разработчик торговой системы может протестировать вариант, при котором комбинации, имеющие высокие значения показателя, получают значительно большую долю капитала, чем им следовало получить при пропорциональном распределении капитала. Соответственно, комбинации с более низкими значениями показателя получают непропорционально меньшую долю капитала. Этого можно добиться путем трансформации линейной весовой функции в выпуклую функцию.
Противоположный сценарий может состоять в том, что в комбинации, имеющие высокие значения показателя, инвестируется меньшая доля капитала, чем при пропорциональном распределении капитала. В таком случае непропорционально большая доля капитала инвестируется в комбинации с низкими значениями показателя. Для достижения такого результата следует трансформировать линейную весовую функцию в вогнутую функцию.
Можно разработать множество математических вариантов решения данной задачи. Продемонстрируем здесь наиболее простой и технически легко реализуемый вариант трансформации линейных функций в вогнутые и выпуклые. Для этого представим весовую функцию в следующем виде:
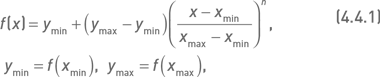
где xi – значение показателя для i-й комбинации,
xmin – значение показателя для комбинации с наименьшим значением показателя,
xmax – значение показателя для комбинации с наибольшим значением показателя.
В дальнейших рассуждениях мы будем полагать ymin = xmin, ymax = xmax. В этом случае, если принять степенной показатель в формуле 4.4.1 равным 1, то весовая функция приобретает вид f(x) = xi, то есть превращается в простую линейную функцию. Для всех n > 1 данная функция является выпуклой (обозначим ее f+(x)), а для всех 0 < n < 1 эта функция будет вогнутой (обозначим ее f–(x)).
Рассмотрим примеры вычисления значений выпуклой и вогнутой весовых функций (для n = 2 и n = 0,5, соответственно) для показателя «математическое ожидание прибыли». Воспользуемся данными, приведенными в таблице 4.3.2, для портфеля, состоящего из 20 акций. Минимальное значение показателя равно 0,0003, а максимальное значение составляет 0,0191. Вычислим значение выпуклой весовой функций для акции AAPL:

Используя степенной показатель n = 0,5, получим для этой же акции значение вогнутой функции: f–(x) = 0,01373. Воспользовавшись формулой 4.3.5, можем рассчитать веса этой комбинации в составе портфеля. Если капитал будет распределяться по выпуклой функции, то вес комбинации AAPL составит 0,082, а если по вогнутой, то 0,072.
Вычислив аналогичным способом значения обеих функций для всех 20 акций, получим два варианта распределения капитала – по выпуклой и вогнутой весовым функциям. На левом графике рис. 4.4.8 показаны значения двух трансформированных весовых функций и оригинальной линейной функции, послужившей исходным материалом для их расчета. Особенностью выпуклой функции является то, что все ее значения (за исключением экстремумов) меньше, чем значения исходной линейной функции. Для вогнутой функции справедливым будет обратное утверждение – все ее значения (за исключением экстремумов) больше, чем значения исходной линейной функции.
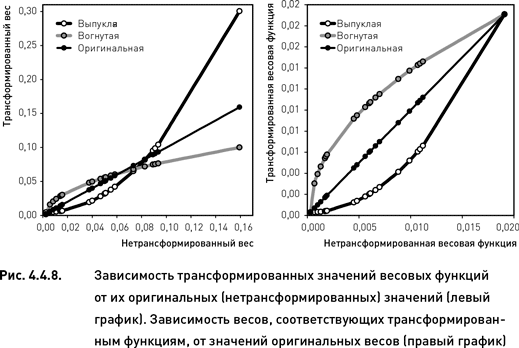
Для наших целей крайне важными будут характеристики чувствительности трансформированных функций к изменениям исходной весовой функции. Ниже мы опишем свойства выпуклой и вогнутой функций по отдельности для низких и высоких значений ее аргумента (исходной, нетрансформированной функции). Эти описания базируются на визуальном анализе левого графика рис. 4.4.8, а также на производных функции 4.4.1. Полагая ymin = xmin, ymax = xmax, производные выпуклой (n = 2) и вогнутой (n = 0,5) функций имеют вид:
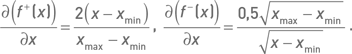
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК