5.1.5. Проверка достоверности данных

Данные, поступающие даже из самых надежных источников, могут оказаться искаженными. Помимо примитивных ошибок, связанных с программными сбоями или техническими проблемами (например, десятичная точка перепутана с запятой, неучтенное переименование тиккера, пропущенная информация о сплите, и т. п.), встречаются систематические ошибки, связанные с неверными и пропущенными котировками. Серьезную проблему представляет несинхронность данных о цене базового актива и соответствующих ему опционов. Эта проблема может быть обусловлена, к примеру, тем, что многие инструменты торгуются на разных биржевых площадках и электронных системах. Моделировать торговлю на основе таких данных чревато серьезными искажениями результатов.

Проблему недостоверных данных необходимо решать путем их выявления и дальнейшего исправления либо фильтрации. Процедуры выявления необходимо применять ко всем поступающим в базу новым ценам и котировкам спроса и предложения. Существуют два подхода к выявлению искаженных данных: тесты на наличие арбитражных ситуаций и исследование поверхностей подразумеваемой волатильности.

В основе тестов на наличие арбитражных ситуаций находится теория ценообразования опционов и условие паритета опционных цен. Для европейских опционов с одинаковой датой экспирации паритет цен опционов пут и колл без учета дивидендов имеет вид равенства:

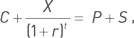
где N – цена опциона колл, P – цена опциона пут, X – страйк опционов, S – текущая цена базового актива, r – безрисковая ставка, t – время до экспирации. Понятие паритета основывается на принципе невозможности возникновения на эффективном рынке арбитражных ситуаций. Другими словами, не может существовать финансового инструмента или совокупности инструментов, с помощью которых можно получить без риска доходность, превышающую безрисковую ставку. Это касается любых опционных комбинаций.

Если выявляется нарушение паритета, то это говорит о том, что цены опционов ошибочны либо существует учтенная в них рынком, но неизвестная проверочному алгоритму информация – например, выплата дивидендов. Ошибочной может быть цена одного из опционов либо обоих. В последнем случае необходимо установить, цена которого из опционов искажена. Для этого следует каждый из двух опционов проверить в паре с другим опционом, успешно прошедшим тест на паритет. Другой опцион будет неизбежно иметь другой страйк либо другую дату истечения. Выявив опцион с искаженной ценой, его следует исключить из базы данных либо исправить цену путем решения уравнения паритета (цена искаженного опциона берется как неизвестное, а цена правильного опциона является константой).

Существенным недостатком данного метода является то, что он применим только для европейских опционов. Для американских опционов формула паритета имеет вид неравенства:

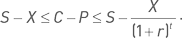
Из формулы следует, что для американских опционов не существует точного значения паритета. Алгоритм тестирования может установить лишь факт попадания разности цен опционов кол и пут в определенный диапазон. Выход за рамки диапазона означает нарушение паритета, однако попадание в диапазон еще не означает, что искажение цены полностью исключается. Цена одного из опционов (либо обоих) может быть неправильной, но не настолько, чтобы выйти за рамки диапазона. Впрочем, и для европейских опционов существует возможность искажения цены при соблюдении паритета. Например, если уменьшить цену пута на некую величину и при этом увеличить цену колла на такую же величину, то условие паритета будет соблюдено, несмотря на то что цены обоих опционов искажены.

Другой метод выявления искаженных данных основывается на расчетах подразумеваемой волатильности. Для этого необходимо вычислить значения подразумеваемой волатильности для всех опционов, относящихся к определенному базовому активу. В силу целого ряда причин эти значения не будут совпадать. Вместе с тем их расхождения не являются случайными. В частности, зависимость подразумеваемой волатильности от страйка в большинстве случаев имеет форму улыбки (она так и называется «улыбкой волатильности») – наименьшее значение соответствует страйку, наиболее близкому к текущей цене базового актива, а по мере удаления страйка в обе стороны (глубоко «в деньгах» и глубоко «вне денег») волатильность возрастает. Могут быть и другие формы зависимости. Однако, какова ни была бы форма зависимости, она представляет собой более-менее гладкую кривую (либо, в отдельных случаях, прямую линию). Если же одна из точек (то есть одно из значений волатильности) выпадает из общего ряда и находится далеко от того места на кривой, где должна находиться, это с большой вероятностью указывает на искажение цены опциона, соответствующего данному страйку.

Можно построить аналогичную зависимость подразумеваемой волатильности от даты экспирации. Однако удобнее всего рассматривать поверхность волатильности, представляющую собой трехмерный график зависимости подразумеваемой волатильности от страйка и даты экспирации. В нормальной ситуации такой график имеет форму относительно гладко изгибающейся поверхности. Острые пики и впадины на такой поверхности указывают на возможно некорректные значения подразумеваемой волатильности, что может свидетельствовать об искажении цены опционов.

Основная проблема данного метода состоит в том, что выявление аномальных цен базируется на визуальном анализе графиков, что абсолютно недопустимо при ежедневном автоматическом пополнении базы данных десятками тысяч новых тиккеров. Решить эту проблему можно с помощью алгоритмизации поиска точек «выброса», что во многих случаях является нетривиальной задачей. При рассмотрении одномерной линейной зависимости (например, волатильности от страйка), эта задача решается просто с помощью линейной аппроксимации. Аномальные точки находятся путем сравнения их остатков (residuals), получаемых из регрессионной модели. Если остаток некой точки отличается от среднего остатка больше, чем на пороговую величину, то это может рассматриваться как индикация искажения цены соответствующего опциона.

В тех случаях, когда зависимость нелинейна (а таких случаев большинство), приходится использовать более сложные модели апроксимации. Задача усложняется еще больше при переходе от одномерной системы к поверхностям волатильности. В этом случае приходится применять еще более сложные математические модели. Главное требование к этим моделям – достаточно точная аппроксимация данных и наличие аналитической формулы, описывающей подбираемую кривую или поверхность.

Формулы требуются для того, чтобы в случае выявления искаженных ценовых значений можно было вычислить корректную цену. Для этого необходимо удалить из модели точку-outlier и вновь рассчитать аналитическую формулу кривой либо поверхности. После этого следует вычислить новое значение подразумеваемой волатильности для данного outlier с помощью новой формулы. Имея скорректированное значение волатильности, можно рассчитать корректную стоимость опциона с помощью выбранной модели ценообразования.