Выпуклая функция
На относительно высоких интервалах значений исходной функции приращение значений выпуклой функции больше, чем на низких интервалах значений исходной функции. Другими словами, разница в значениях трансформированной функции между комбинацией с наибольшим значением показателя и комбинацией со вторым по величине значением показателя больше, чем разница в значениях трансформированной функции между комбинацией со средним или низким значением показателя и комбинацией с предыдущим значением показателя. Кроме того, на высоких интервалах значений исходной функции приращение значений выпуклой функции больше, чем приращение значений самой исходной функции. Формально это можно выразить следующим образом. Обозначим через x(Ci) значение показателя i-й комбинации. Пусть портфель состоит из m комбинаций {C1, C2…, Cm}. Причем x(Cm) > x(Cm – 1), x(Cm – 1) > x(Cm – 2) и так далее. Тогда для выпуклой функции соблюдаются неравенства:
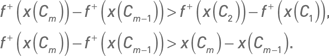
На низких интервалах значений исходной функции приращение значений выпуклой функции меньше, чем на высоких интервалах значений. Разница в значениях трансформированной функции между комбинацией со вторым по величине значением показателя и комбинацией с первым (самым низким) значением показателя меньше, чем разница в значениях трансформированной функции между комбинацией со средним или высоким значением показателя и комбинацией с предыдущим значением показателя. Кроме того, на низких интервалах значений исходной функции приращение значений выпуклой функции меньше, чем приращение значений самой исходной функции. Формально это можно выразить следующими неравенствами:
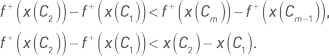
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК