Анализ эффективности использования индексной дельты для оценки риска

Для исследования эффективности индексной дельты нами проведены статистические исследования на исторической базе данных, содержащей восьмилетнюю историю цен опционов и их базовых активов. В качестве базовых активов были задействованы акции, составляющие индекс S&P 500.

На историческом горизонте с начала 2001 г. по начало 2009 г. для каждой даты экспирации была сформирована серия портфелей. Момент создания каждого портфеля отстоял от даты экспирации на разное количество торговых дней. Так, самый «дальний» из портфелей был удален от даты истечения на 60 дней, следующий за ним – на 59 дней и так далее вплоть до последнего портфеля, отстоящего от момента экспирации всего на два дня. Таким образом, на каждую дату экспирации было создано 59 портфелей, отличающихся друг от друга продолжительностью времени, остающегося до дня истечения опционов. Всего было создано от 30 (для 60 дней) до 90 (для двух дней) портфелей для каждого «количества дней до экспирации».

Каждый портфель состоял из коротких стрэддлов для всех акций, входящих в состав указанного индекса. Страйк стрэддлов выбирался по принципу наименьшей удаленности от текущей цены БА. Объем позиции по каждому стрэддлу вычислялся как округленная до лотов (1 лот = 100 опционов) величина N = 10 000/U, где U – цена акции, являющейся БА для данного стрэддла. Бета каждой акции вычислялась по 120-дневной выборке доходностей акции и индекса. Дельты опционов ?_i рассчитывались по модели Блэка – Шоулса; процентные индексные дельты D^%_Portfolio – по формуле (3.2.4). Кроме того, для каждого портфеля вычислялись следующие величины:

• Процентное изменение индекса I^% = 100 ? (I_e – I_t)/I_t, где I_t – значение индекса на момент t создания портфеля, I_e – значение индекса на момент истечения опционов.

• Процентное изменение стоимости портфеля P^%_realized = 100 ? (P_e ? P_t)/P_t где P_t – рыночная стоимость портфеля на момент t создания портфеля, P_e – стоимость портфеля на момент истечения опционов (премии опционов брались в середине спреда цены спроса и предложения). Этот показатель выражает «реализовавшийся» риск портфеля.

• Ожидаемое процентное изменение стоимости портфеля P^%_expected = 100 ? (I^%? D^%_Portfolio)/P_t. Этот показатель выражает оценку риска сложноструктурированного портфеля при условии, что индекс изменится на заданную величину (в данном исследовании – на величину реально произошедшего движения рынка).

• Разность реализовавшегося изменения стоимости портфеля и ожидаемого изменения стоимости портфеля Difference = P^%_realized – P^%_expected. Чем ближе к нулю этот показатель (то есть чем меньше абсолютное отклонение реализовавшегося изменения от ожидаемого), тем точнее индексная дельта позволяет прогнозировать будущие колебания стоимости портфеля.

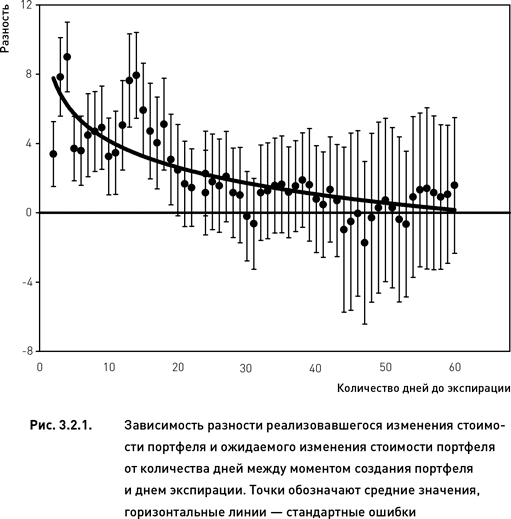
На рис. 3.2.1 показаны средние отклонения реально произошедших изменений стоимости портфеля от ожидаемых значений. Для портфелей, созданных в период от 30 до 60 дней до экспирации, средняя разность оказалась близка к нулю. Однако этим же портфелям свойственна и наибольшая изменчивость разности (представленная на рис. 3.2.1 в виде стандартных ошибок). Обратная картина наблюдается для портфелей, созданных незадолго до экспирации (от двух до 20 дней). В этих случаях разности реализовавшегося и ожидаемого изменений стоимости портфеля велики и положительны, хотя достаточно стабильны (стандартные ошибки невелики).

Положительные значения разности говорят о том, что P^%_realized > P^%_expected (реализовавшиеся изменения стоимости портфеля больше, чем ожидалось). Это означает, что оценка риска с помощью индексной дельты для этих портфелей была заниженной, то есть риск оказался недооценен (поскольку убыток коротких портфелей возникает в тех случаях, когда их стоимость возрастает (P^%_realized > 0)). Соответственно, отрицательное значение разности означает, что реальные изменения стоимости портфеля оказались меньше, чем ожидалось (то есть риск был переоценен). Поскольку стандартные ошибки портфелей, созданных задолго до экспирации, далеко заходят как в отрицательную, так и в положительную область (рис. 3.2.1), можно заключить, что многие из них были переоценены и многие – недооценены.

В целом можно сделать вывод, что в момент создания портфеля чем больше срок до даты истечения опционов, тем более точно (в среднем) оценивается риск. Вместе с тем вероятность ошибочных оценок также возрастает. Для портфелей, создаваемых вблизи экспирации, оценка риска оказывается заниженной, однако величина занижения является достаточно стабильной (вероятность ошибки мала). В первом случае можно добиться повышения эффективности использования индексной дельты путем введения дополнительных показателей риска. Во втором случае, поскольку изменчивость результатов невелика, можно ограничиться введением поправочных коэффициентов.

Известно, что дельта является локальной величиной, оценивающей изменение стоимости опциона при небольшом изменении цены его базового актива. Это означает, что чем больше реально произошедшее изменение цены базового актива, тем менее точен прогноз изменения стоимости опциона, основанный на дельте. Исследуем, справедливо ли данное утверждение для индексной дельты и насколько ухудшается эффективность ее прогноза при больших изменениях индекса. Для этого рассмотрим зависимость разностей между реализовавшимися и ожидаемыми изменениями стоимости портфеля от процентного изменения индекса.

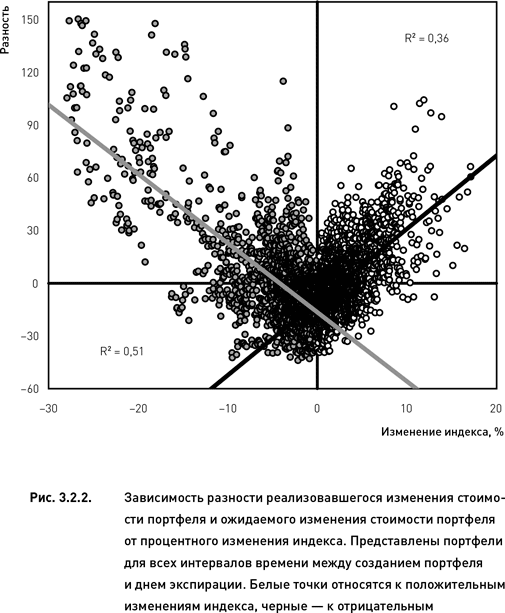
Из рис. 3.2.2 следует, что большие движения индекса действительно сопровождаются весьма серьезными отклонениями реальных изменений стоимости портфелей от прогнозных значений. Это наблюдение справедливо как для случаев роста индекса (белые точки на рис. 3.2.2), так и для случаев его падения (черные точки). Следует также отметить, что в тех случаях, когда индекс снижался, корреляция между разностью и изменением индекса была выше, чем когда индекс рос.

Для оценки эффективности индексной дельты наибольший интерес представляет тот факт, что большим движениям индекса (будь то рост или падение) соответствуют только положительные разности, в то время как малым – в основном отрицательные (рис. 3.2.2). Это говорит о том, что при больших движениях рынка индексная дельта недооценивает риск, а при малых – переоценивает. В тех же случаях, когда амплитуда колебаний рынка находится в пределах 3–5 % (в сторону роста или понижения), индексная дельта демонстрирует наибольшую эффективность.

В предыдущем исследовании мы ограничились случаями, когда риск оценивается только один раз – в момент создания портфеля. Эффективность этой оценки тестировалась также единожды – на дату истечения входящих в состав портфеля опционов (предполагается, что все опционы истекают одновременно). Теперь мы исследуем ситуации, когда риск оценивается регулярно в течение всего периода существования портфеля, а эффективность оценки тестируется на разных временных интервалах.

Мы будем оценивать эффективность индексной дельты так же, как в предыдущем исследовании (путем сравнения оценки риска, выраженного через индексную дельту, со значениями, реализовавшимися на практике). Чтобы проанализировать качество прогноза на разных этапах существования портфеля, следует (1) вычислять значения индексной дельты каждый день на протяжении всего инвестиционного периода и (2) оценивать изменения стоимости портфеля в течение разных периодов времени (будем называть их горизонтами тестирования или прогнозирования). Необходимо протестировать все периоды от первого дня до максимально возможного (49 дней в нашем исследовании). Эти данные позволят всесторонне оценить расхождения между прогнозами и реальностью.

Для каждой даты экспирации был сформирован портфель, состоящий из коротких стрэддлов для всех 500 акций, входящих в S&P 500. Момент создания каждого портфеля отстоял от даты истечения формирующих его опционов на 50 торговых дней. Всего было создано 90 таких портфелей. Страйк стрэддлов выбирался по принципу наименьшей удаленности от текущей цены базового актива. Объем позиции по каждому стрэддлу рассчитывался как округленная до лотов (1 лот = 100 опционов) величина, где U – цена акции, являющейся базовым активом для данного стрэддла.

В таблице 3.2.2 представлен пример такого портфеля и показана эволюция его показателей. В момент создания портфеля (7 августа 2008 г., первая строка таблицы) оставалось 50 рабочих дней до даты экспирации опционов (17 октября 2008 г.). Во второй строке таблицы приведены характеристики этого же портфеля на следующий день после его создания, в третьей строке – на третий день и т. д. вплоть до экспирации (в целях экономии места в таблице 3.2.2 показаны только первые 20 дней существования портфеля).

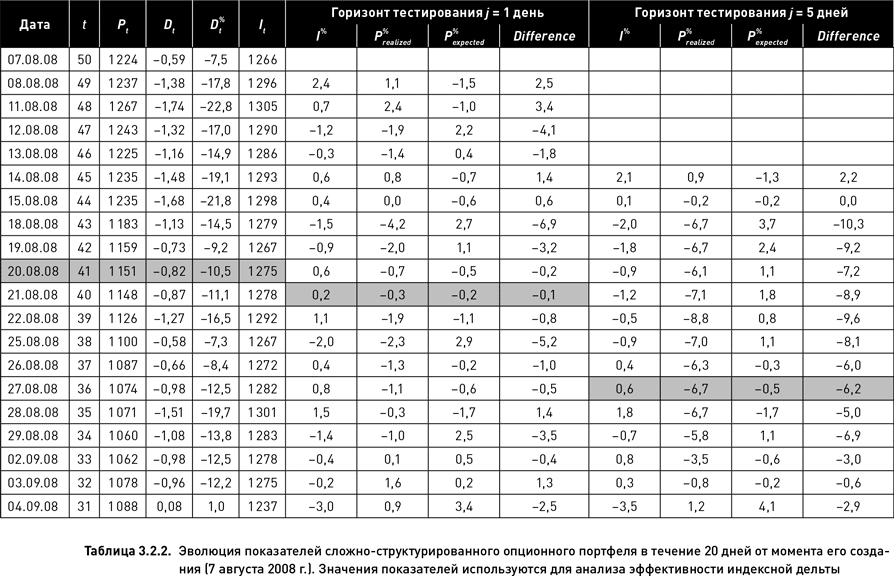
В таблице приводятся значения следующих показателей, необходимых для оценки разности между прогнозным и реализовавшимся значением риска.

• Количество дней, остающихся до экспирации t (используется для индексирования моментов оценки и тестирования).

• Рыночная стоимость портфеля P_i на момент оценки t; вычисляется как сумма стоимостей всех входящих в состав портфеля опционов.

• Индексная дельта D_i, рассчитанная на момент t с помощью формулы (3.2.1).

• Процентная индексная дельта D^%_t = I_t D_t / 100, рассчитанная на момент t; прогнозирует изменение стоимости портфеля при изменении индекса на 1 %.

• Значение индекса I_t на момент оценки t и процентное изменение индекса I^% = 100(I_t?j ? I_t) / It ? где I_t?j – значение индекса на момент тестирования; j выражает количество дней между двумя датами t и t-j и является горизонтом тестирования.

• Процентное изменение стоимости портфеля P^%_realized = 100(P_t?j ? P_t) / P_t, где P_t – рыночная стоимость портфеля на момент оценки t, P_t?j – стоимость портфеля на момент тестирования. Этот показатель выражает изменение стоимости портфеля, произошедшее в течении j дней, и является, по сути, риском портфеля, реализовавшимся на определенном горизонте тестирования. Напомним, что рост стоимости опционов короткого портфеля (то есть положительное изменение его стоимости) приносит убыток, а снижение их стоимости дает прибыль.

• Ожидаемое процентное изменение стоимости портфеля P^%_expected = 100 I^%D^%_Portfolio / P_t. Этот показатель выражает оценку риска сложноструктурированного портфеля при условии, что в течении j дней индекс изменится на величину I^%.

• Разность реализовавшегося изменения стоимости портфеля Difference = P^%_realized ? P^%_expected и ожидаемого изменения стоимости портфеля. Положительные значения разности указывают на недооценку риска индексной дельтой; отрицательные разности свидетельствуют о переоценке риска. Соответственно, чем ближе к нулю этот показатель, тем точнее индексная дельта позволяет прогнозировать будущие колебания стоимости портфеля.

В таблице 3.2.2 приведены расчеты для двух горизонтов тестирования – один и пять дней. Возьмем для примера 41-й день до экспирации (t = 41, выделено серым цветом в таблице) и проделаем поэтапно все вычисления, необходимые для оценки разности между прогнозируемым и реализовавшимся риском. Индексная дельта в этот день оценки равна:

Для горизонта тестирования j = 1 процентное изменение индекса составляет:

Процентное изменение стоимости портфеля равно:

а ожидаемое процентное изменение стоимости портфеля составляет:

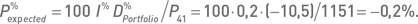
Разность реализовавшегося и ожидаемого изменений стоимости портфеля равна:

что указывает на небольшую переоцененность риска в данном случае. Для горизонта тестирования j = 5 процентное изменение индекса составило:

Изменение стоимости портфеля равно:

а ожидаемое процентное изменение стоимости портфеля оказалось равным:

Разность реализовавшегося и ожидаемого изменений стоимости портфеля в этом случае была намного большей и составила:

что указывает на существенную переоцененность риска. Аналогичным образом были рассчитаны все 90 портфелей. Риск каждого из них оценивался ежедневно в течение всех 50 дней существования портфеля. Эффективность этих оценок тестировалась на всех горизонтах от одного до 49 дней.

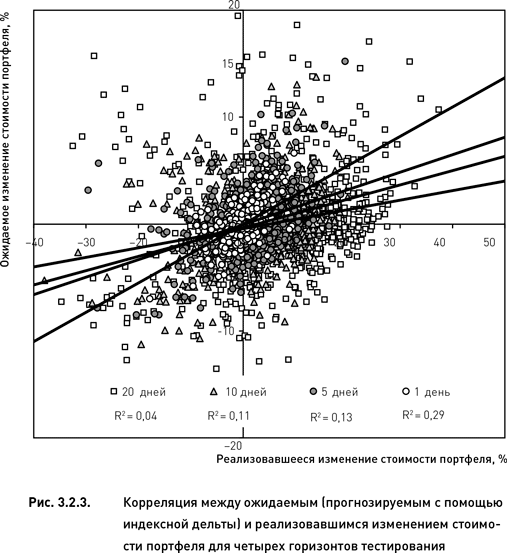
Взаимозависимость показателей прогнозируемого и реализовавшегося риска дает наглядное представление о степени эффективности индексной дельты. Рис. 3.2.3 демонстрирует такую зависимость для начального этапа существования портфелей (с 50-го по 40-й день до экспирации). Наибольшая корреляция обнаружена для однодневного горизонта тестирования. В этом случае «размытость» облака точек оказалась наименьшей (коэффициент корреляции R? = 0,29 наибольший). Удлинение горизонта тестирования до 5, 10 и 20 дней привело к постепенной деградации качества прогноза. Визуальный анализ рис. 3.2.3 показывает, что чем больше был горизонт тестирования, тем слабее становилась зависимость между прогнозом и результатом вплоть до полного исчезновения всякой зависимости (для 20 дней R? = 0,04). Кроме того, увеличение горизонта тестирования сопровождалось уменьшением угла наклона соответствующей регрессии. Это также свидетельствует об ухудшении прогнозных качеств индексной дельты на больших горизонтах тестирования.

Регрессионный анализ, представленный на рис. 3.2.3, является наиболее простым и интуитивно понятным средством качественной оценки индексной дельты. Вместе с тем он не дает строгого количественного выражения эффективности этого индикатора риска. Для этих целей лучше подходит средняя разность реализовавшихся и ожидаемых изменений стоимости портфеля. Поскольку убыток коротких портфелей возникает в тех случаях, когда их стоимость возрастает P^%_realized > 0, положительные разности (P^%_realized > P^%_expected) свидетельствуют о том, что оценка риска с помощью индексной дельты занижена (то есть риск недооценен). Соответственно, отрицательные разности означают, что реальные изменения стоимости портфеля меньше ожидавшихся (то есть риск переоценен).

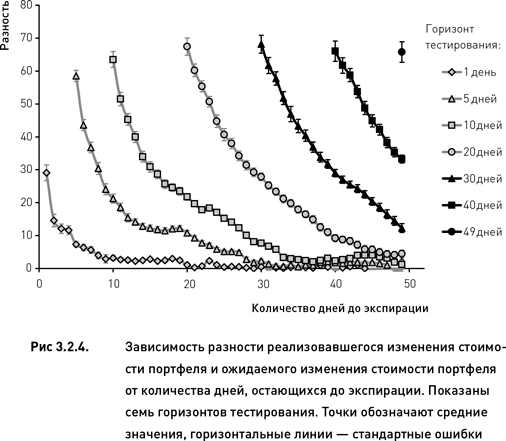
На рис. 3.2.4 показаны средние разности и стандартные ошибки (выражающие меру изменчивости результатов) для разных горизонтов тестирования. Для наиболее эффективного однодневного горизонта тестирования отклонения реально произошедших изменений стоимости портфелей от прогнозных значений были близки к нулю на всем периоде от создания портфелей до приблизительно 20-го дня до экспирации. После 20-го дня чем ближе портфель приближался к дате экспирации, тем более недооцененным оказывался риск. Таким образом, индексная дельта позволяет достаточно точно прогнозировать риск, но на весьма короткий промежуток времени (один день) и только на раннем и среднем этапах существования портфеля (в течение 30 рабочих дней с момента его формирования). Пятидневный горизонт тестирования дал похожие результаты, с той разницей, что в этом случае недооценка риска начала возникать уже с 30-го дня до экспирации и достигла более высоких значений. Дальнейшее увеличение горизонта тестирования способствовало еще большему усилению этих тенденций – недооценка риска начиналась раньше и достигала больших значений (рис. 3.2.4). Кроме того, легко заметить, что для коротких горизонтов тестирования зависимость между разностью и количеством дней до экспирации является нелинейной. В то же время для больших горизонтов тестирования эта зависимость постепенно становится линейной и все более «крутой». В данном случае крутизна наклона линии регрессии характеризует скорость деградации прогноза по мере приближения даты истечения опционов.

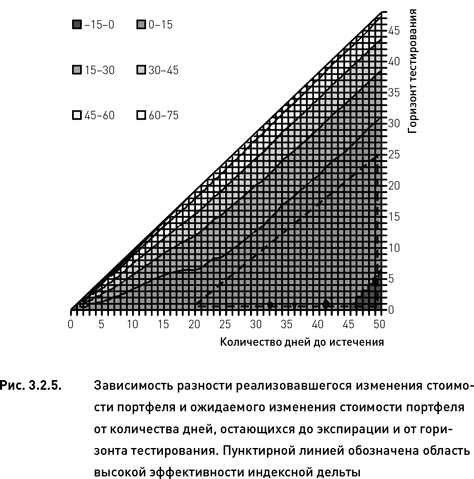
Полную информацию об эффективности индексной дельты и характере ее зависимости от двух исследуемых параметров (момента оценки и горизонта тестирования) дает представление данных в виде топографической карты. В двумерной системе координат будем откладывать по горизонтальной оси количество дней, остающихся до экспирации, а по вертикальной – горизонт тестирования. С помощью разных оттенков изобразим изолинии, отражающие средние разности реализовавшихся и ожидаемых изменений стоимости портфелей. Топография такой поверхности показана на рис. 3.2.5. Легко заметить, что область высокой эффективности индексной дельты располагается в правом нижнем углу диаграммы (показана на рисунке пунктирной линией). В целом можно заключить, что (1) индексная дельта позволяет довольно точно оценивать риск в первые 25–30 дней с момента создания портфеля; (2) эффективность этих оценок сохраняется в течение 20–25 дней с момента оценки. Треугольная форма зоны высокой эффективности указывает на то, что, с одной стороны, по мере приближения экспирации необходимо снижать горизонт прогнозирования. С другой стороны, использование больших горизонтов прогнозирования возможно лишь на начальном этапе существования портфеля.